Matrices
key notes:
Definition
- A set of numbers or objects or symbols represented in the form of a rectangular array is called a matrix.
- The order of the matrix is defined by the number of rows and number of columns present in the rectangular array of representation.
- Unlike determinants, it has no value.
- A matrix of order m × n, i.e. m rows and n columns, is represented below:

- Abbreviated as: A = [aij]m × n, where 1 ≤ i ≤ m; 1 ≤ j ≤ n, i denotes the row and j denotes the column.
- The number a11, a12, ….. etc., are known as the elements of matrix A, where aij belongs to the ith row and jth column and is called the (I,j)th element of the matrix A = [aij].
Type of Matrices
- Row Matrix: Matrix having one row i.e. matrix of order 1 × n. They are also known as row vectors.
- Example: A = [a11 , a12, …… a1n]
- Column Matrix: Matrix having one column i.e. matrix of order m × 1. They are also known as column vectors.
- Example:

- Zero or Null Matrix: An m × n matrix all whose entries are zero. It is denoted as Om×n.
- Example:

- Example:
- Horizontal Matrix: A matrix of order m × n is a horizontal matrix if n > m.
- Example:

- Vertical Matrix: A matrix of order m × n is a vertical matrix if m > n.
- Example:

- Square Matrix: If a number of rows is equal to a number of columns, then the matrix is a square matrix.
- Example:

💡Note: In a square matrix, (a) The pair of elements aij & aji are called Conjugate Elements. Example: a12 and a21 (b) The elements a11, a22, a33, …… ann are called Diagonal Elements. The line along which the diagonal elements lie is called the “Principal or Leading” diagonal. (c) Sum of all the diagonal elements, i.e. Σ aii is known as trace of the matrix. It is denoted as tr(A). |
Diagonal Matrix: A square matrix in which all the elements are zero except the diagonal element. It is denoted as dia(d1, d2, ….., dn).
Example:


| 💡 Note: Min. number of zeros in a diagonal matrix of order n = n(n – 1) |
- Scalar Matrix: A square matrix in which every non-diagonal element is zero and all diagonal elements are equal, is called a scalar matrix.
- i.e. in scalar matrix, aij = 0, for i ≠ j and aij = k, for i = j
- Example:

- Unit/Identity Matrix: A square matrix, in which every non-diagonal element is zero and every diagonal element is 1, is called, unit matrix or an identity matrix.
- i.e. in scalar matrix, aij = 0, for i ≠ j and aij = 1, for i = j
- Example:

| 💡 Equality of Matrices A = [aij] & B = [bij] will be equal, only if 🥏Both have the same order 🥏ai j = bi j for each pair of i & j |
Learn with an example
what are the dimensions of this matrix ?
[ 2 3 0]
_____ by _____
- This matrix has 1 row and 3 columns, so the dimensions are 1 by 3.
Is this an identity matrix?
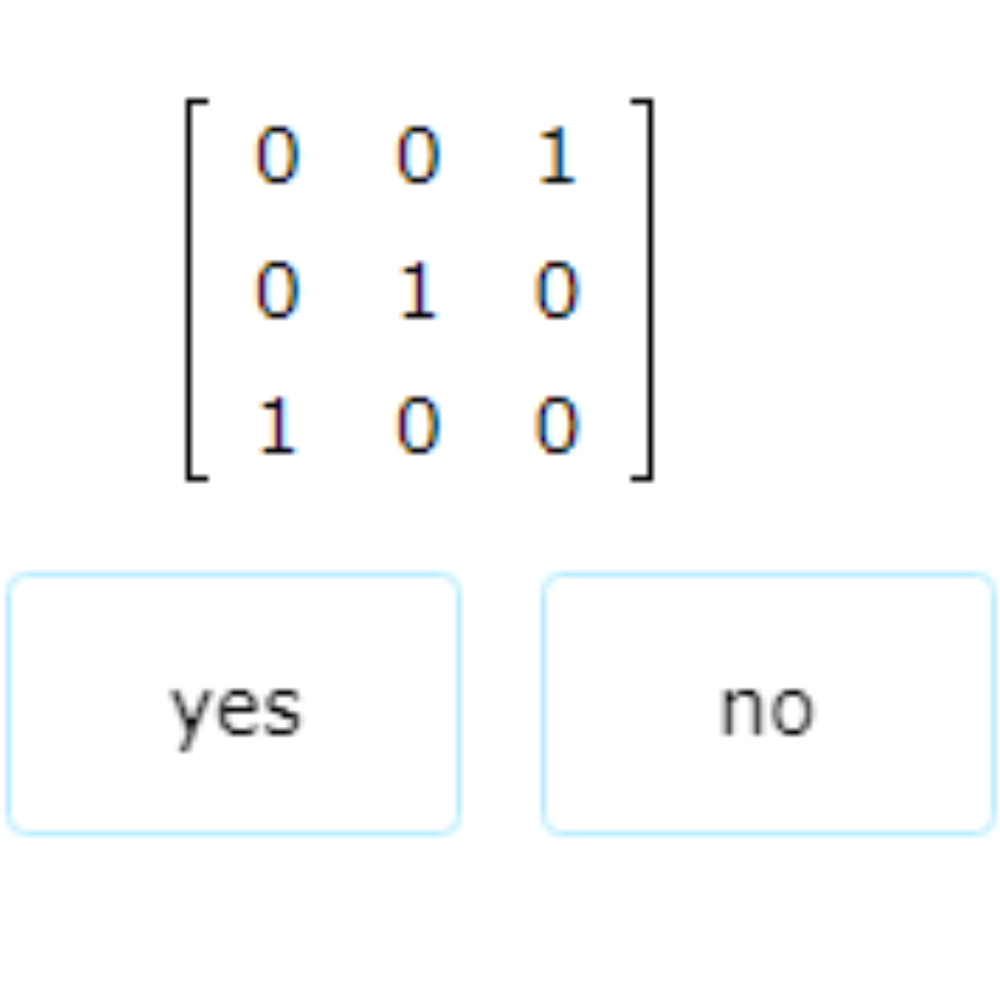
Look at the given matrix.
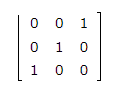
This matrix has 1s on the diagonal from the top right to the bottom left instead of the diagonal from the top left to the bottom right, so it is not the identity matrix.
Is this a row matrix?
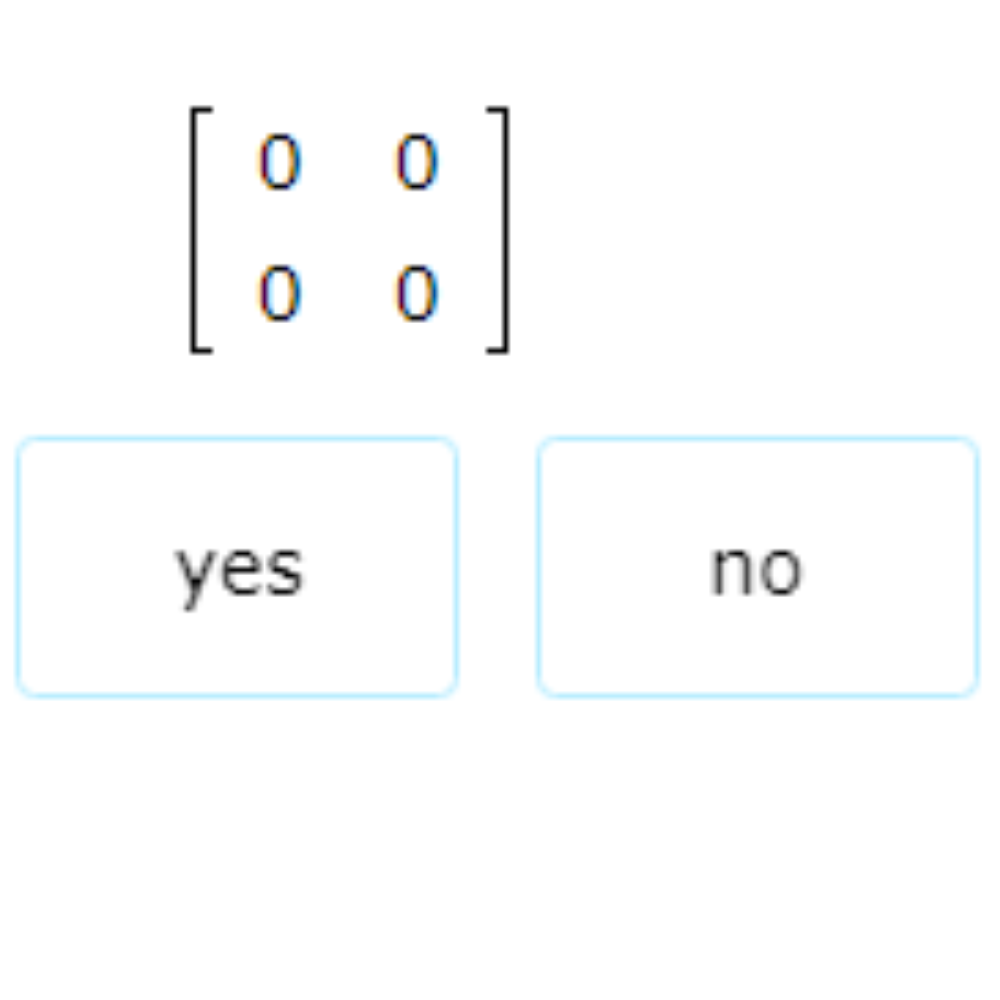
Look at the given matrix.
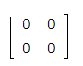
This matrix has 2 rows, so it is not a row matrix.
let’s practice:

