Solve a pair of equations by graphing: word problems
key notes:
A system of two equations can be classified as follows:
If the two lines are parallel, the system is inconsistent, with no solution.
If the two lines intersect at one point, the system is consistent and independent, with one solution.
If the two lines are the same, the system is consistent and dependent, with infinitely many solutions.
Learn with an example
Graph these equations:
y=2x+1
y=2x+6
Click to select points on the graph.
How many solutions do the simultaneous equations have?
- no solution
- one solution
- infinitely many solutions
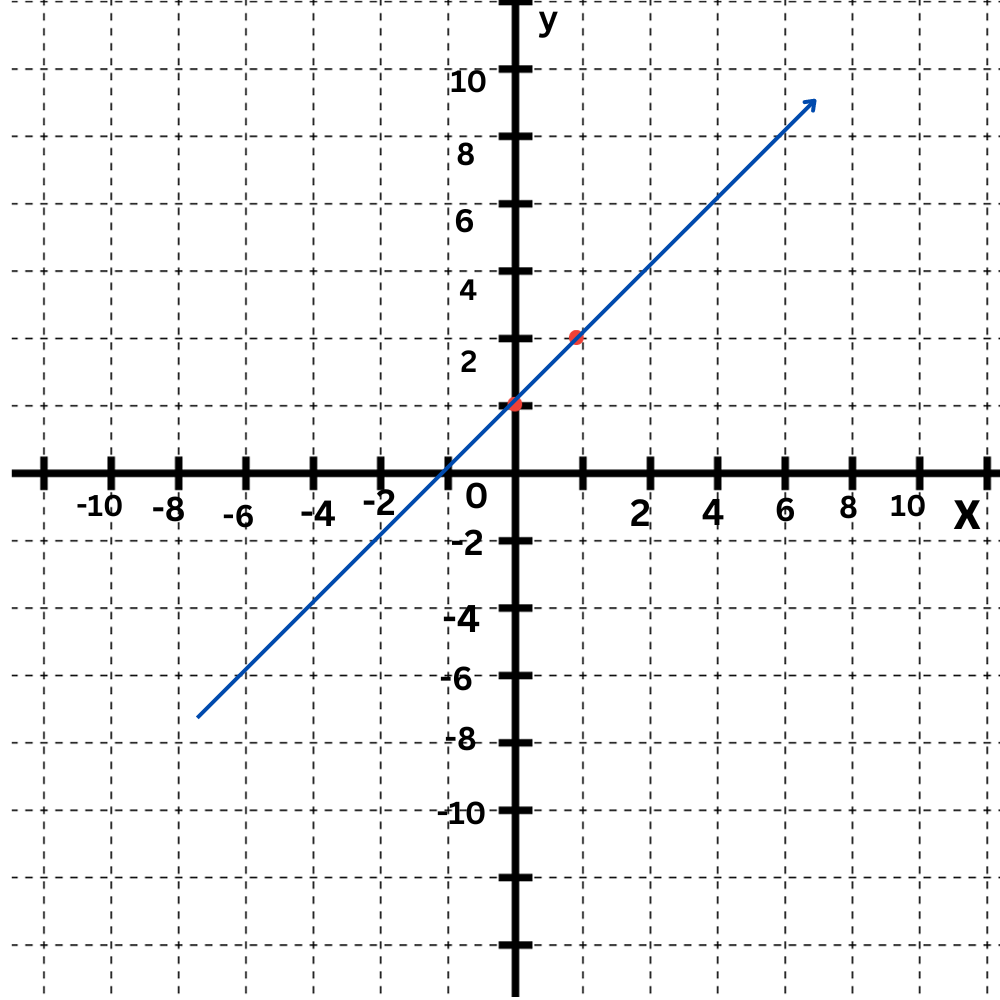
The first equation is y=2x+1.
The y-intercept is 1. Plot the point (0,1).
The slope is 2. Move up 2 and right 1 to find another point on the line.
Draw a line connecting them.
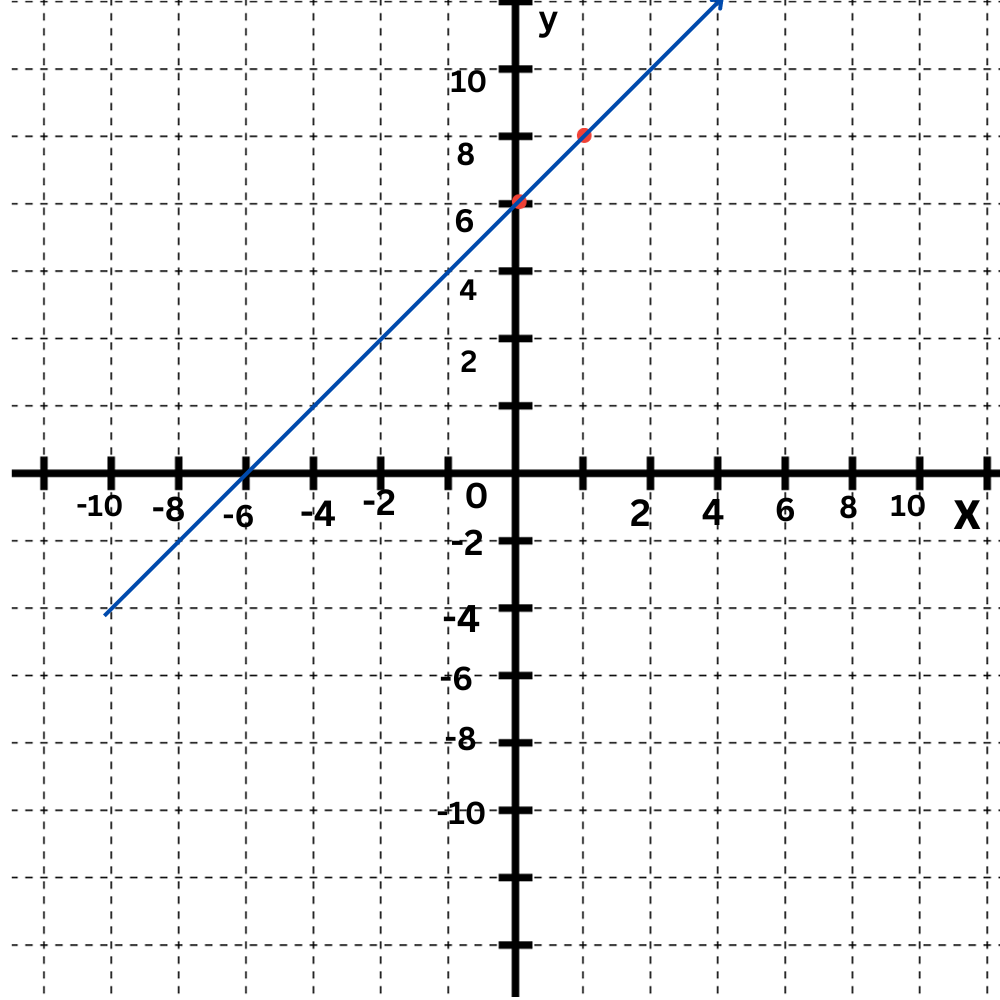
The second equation is y=2x+6.
The y-intercept is 6. Plot the point (0,6).
The slope is 2. Move up 2 and right 1 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
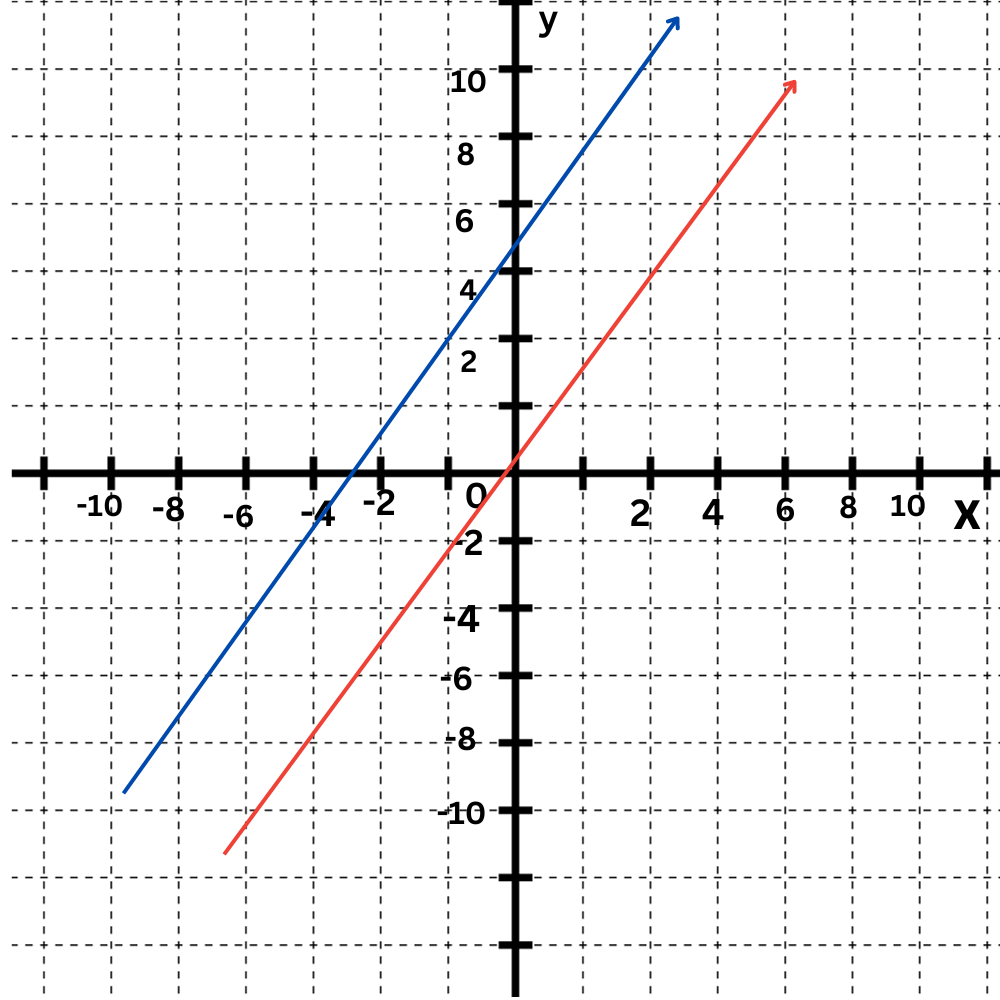
The two lines are parallel. The system has no solution.
Graph these equations:
y=1/6x+1
y=1/6x–4
Click to select points on the graph.
How many solutions do the simultaneous equations have?
- no solution
- one solution
- infinitely many solutions
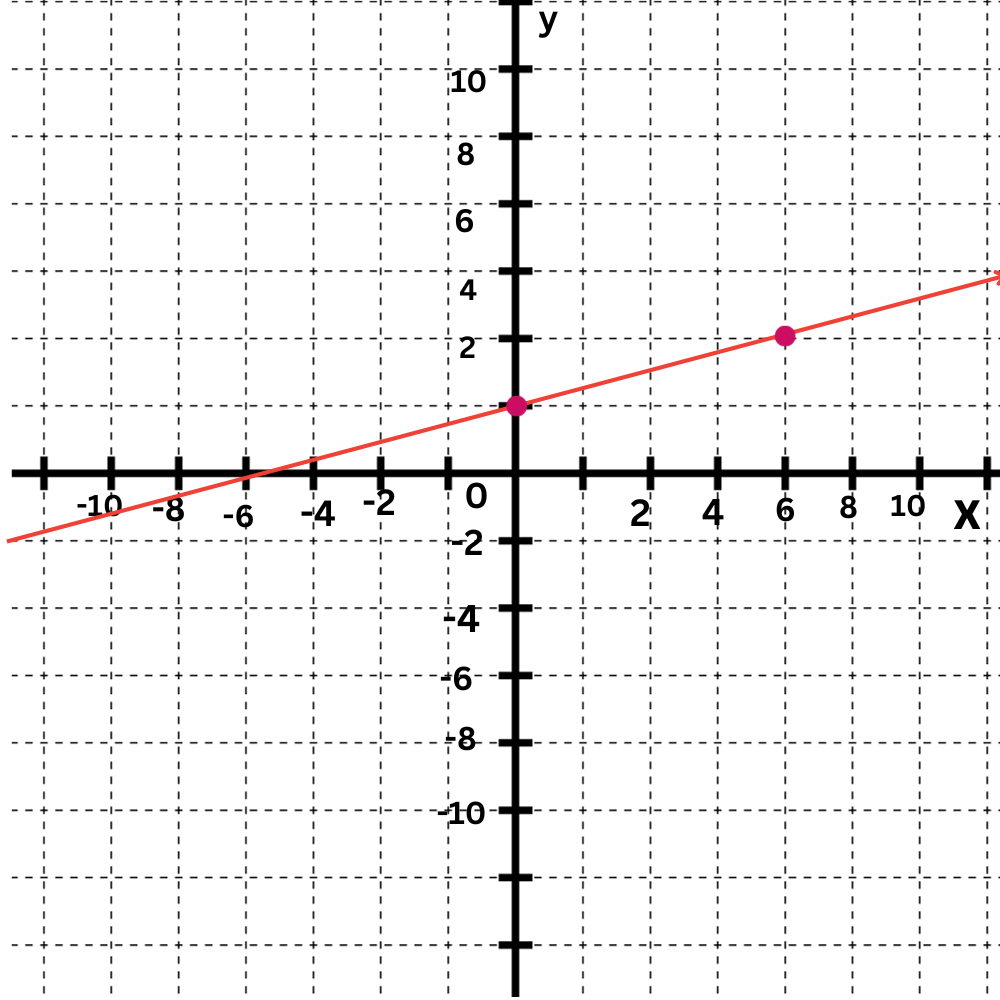
The first equation is y=1/6x+1.
The y-intercept is 1. Plot the point (0,1).
The slope is1/6. Move up 1 and right 6 to find another point on the line.
Draw a line connecting them.
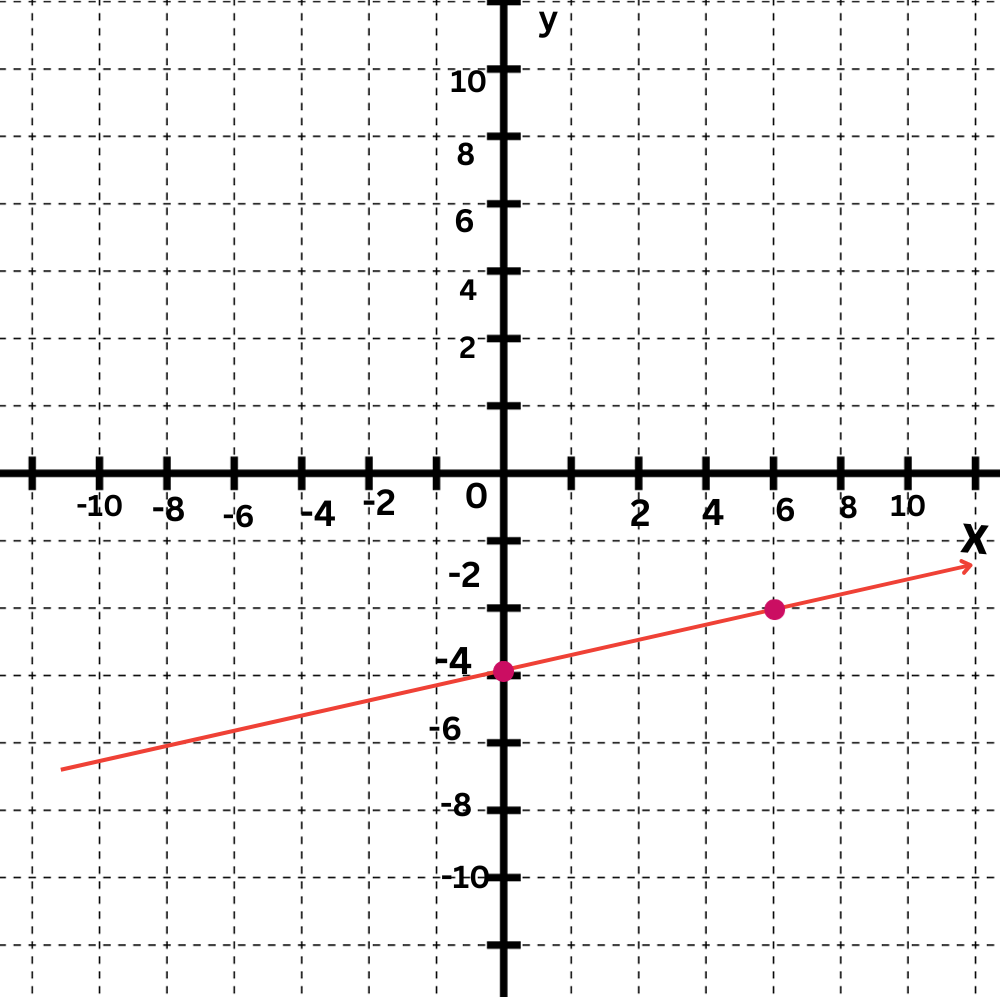
The second equation is y=1/6x–4.
The y-intercept is–4.Plot the point (0,–4).
The slope is1/6. Move up 1 and right 6 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
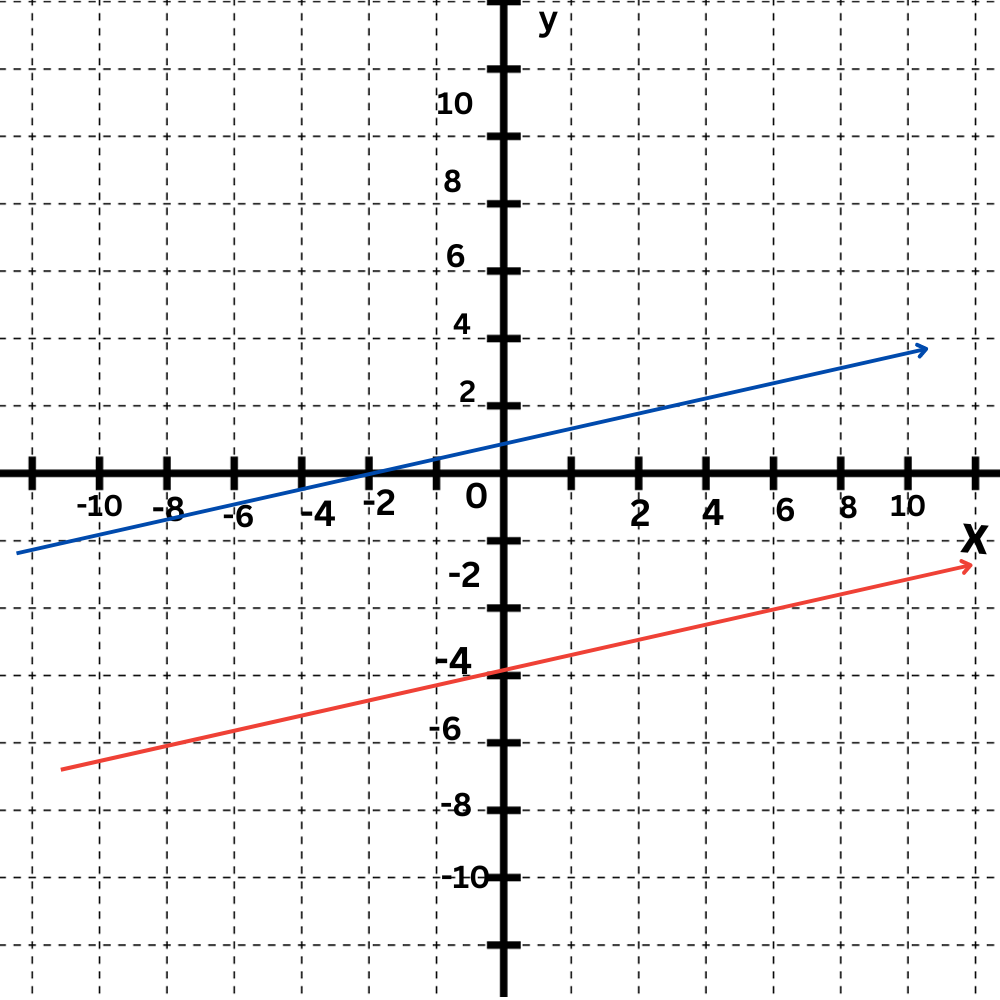
The two lines are parallel. The system has no solution.

