Solve a pair of equations by graphing: word problems
key notes:
- Identify Variables: Understand the problem and identify the variables involved. Assign variables to the unknown quantities mentioned in the problem.
- Set Up Equations: Write down the equations based on the information given in the word problem. Translate the problem into a system of two equations.
- Graph the Equations: Plot the graphs of the two equations on the same set of axes. This involves choosing appropriate scales for the x and y-axes.
- Find the Intersection Point: The solution to the system of equations is the point where the graphs intersect. This point represents the values that satisfy both equations simultaneously.
- Check the Solution: Verify that the values obtained from the intersection point satisfy both original equations in the word problem. This step ensures the accuracy of the solution.
- Interpret the Solution: In the context of the word problem, interpret the solution. What do the values of the variables represent in the real-world scenario described in the problem?
- Consider Constraints: Some problems may have constraints or limitations. Make sure to consider any specified conditions or restrictions on the variables.
- Practice with Different Types of Problems: Solve various word problems to gain proficiency in applying the graphing method to different scenarios. This helps reinforce the understanding of the process.
- Use Technology Wisely: While graphing manually can be educational, utilizing graphing calculators or graphing software can expedite the process and allow for more complex problems.
- Review and Reflect: After solving the problem, review the steps taken and reflect on the process. Understand the connection between the graphical representation and the algebraic solution.
Learn with an example
Mr. Davies, the owner of two car dealerships in Mahuvar, is holding a contest to see which one can sell the most cars. Mahuvar Cars has already sold 10 cars, and Davies’s Autos has sold 20 cars. Going forward, the salespeople at Mahuvar Cars think they can sell 5 cars per day, whereas the salespeople at Davies’s Autos are aiming for sales of 3 cars per day. If the salespeople’s predictions are accurate, it won’t be long before the two dealerships are tied.
How long will that take?
Write simultaneous equations, graph them, and type the solution.
____ Days
Start by writing simultaneous equations. Let x=days and y=cars.
y=5x+10
y=3x+20
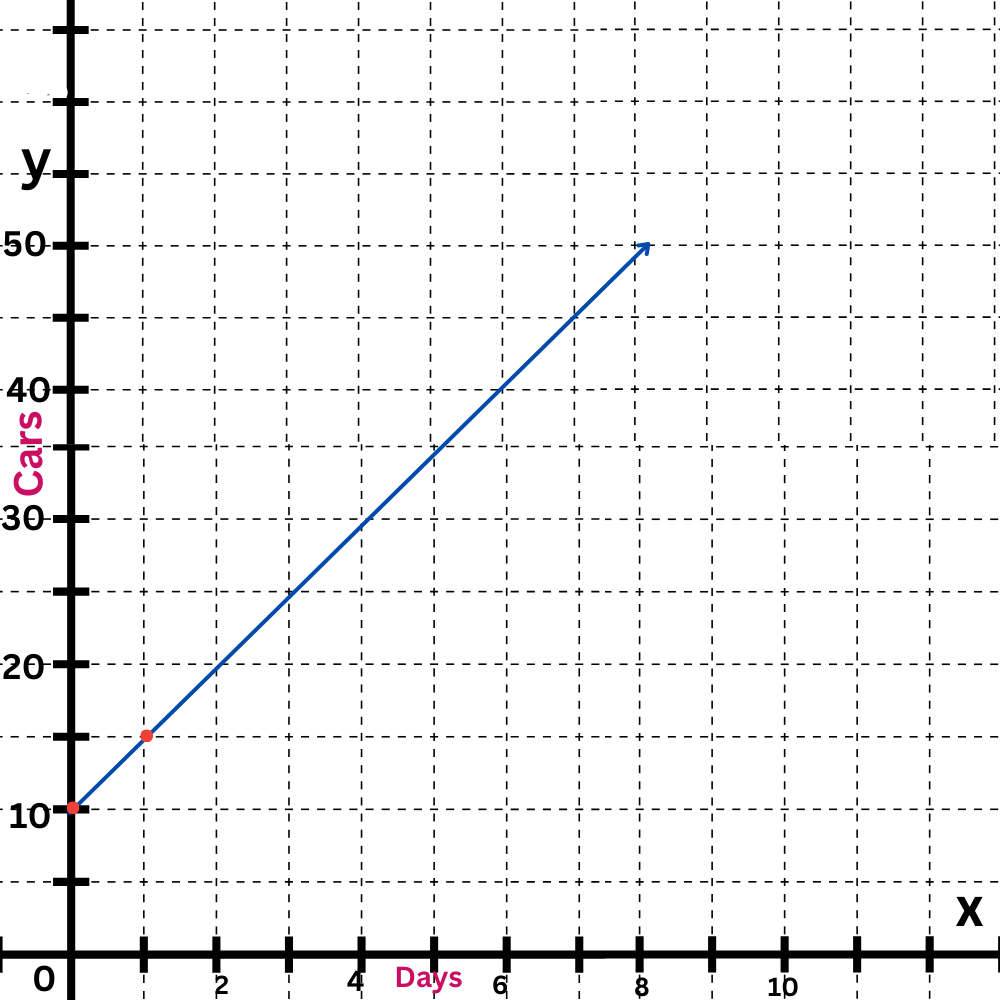
The first equation is y=5x+10.
The y-intercept is 10. Plot the point (0,10).
The slope is 5. Move up 5 and right 1 to find another point on the line.
Draw a line connecting them.
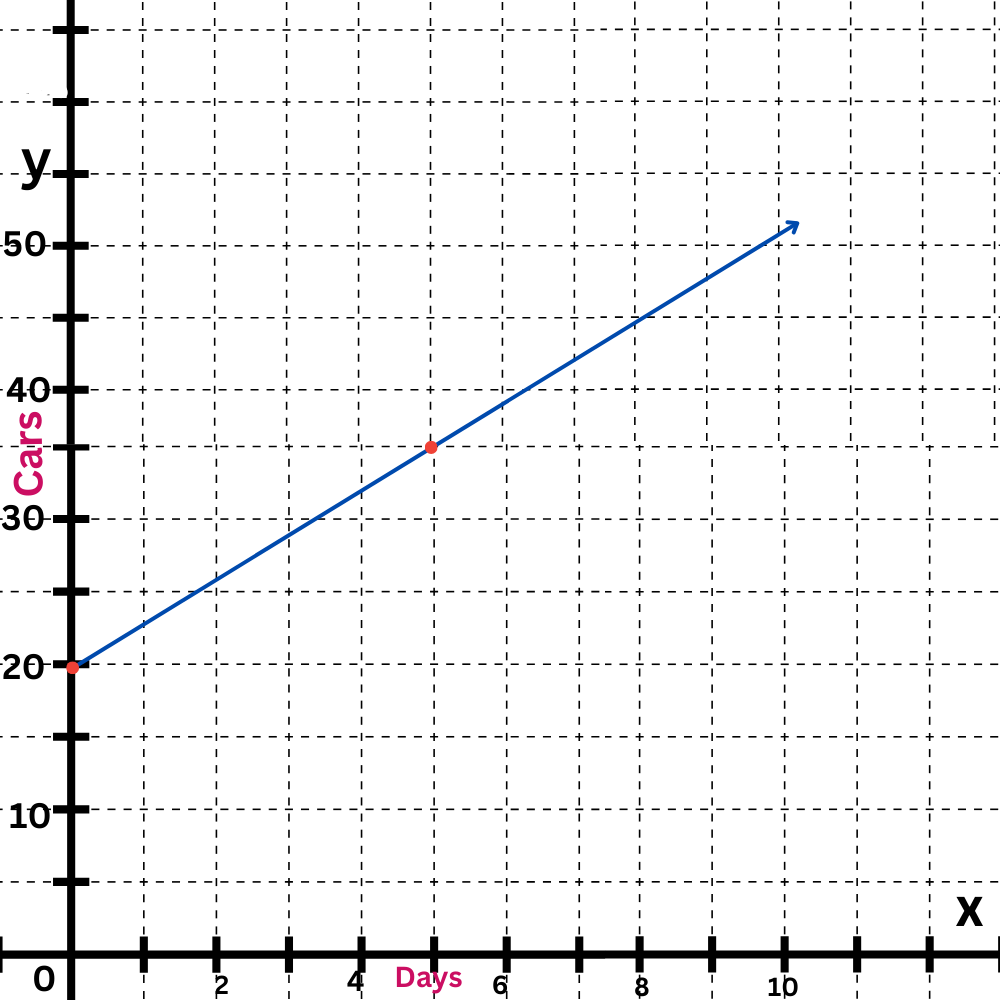
The second equation is y=3x+20.
The y-intercept is 20. Plot the point (0,20).The slope is 3, which is the same as
15/5. Move up 15 and right 5 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
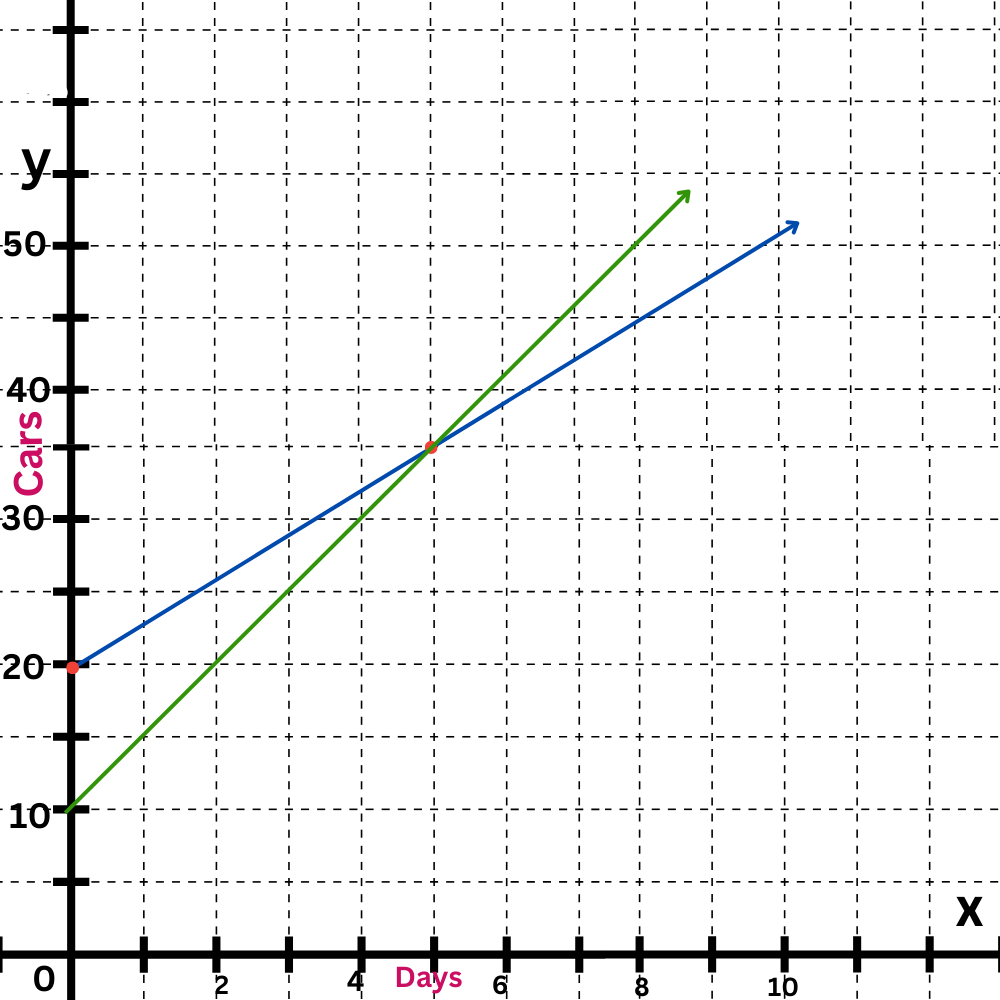
The lines intersect at (5,35).
In 5 days, the dealerships will each have sold 35 cars.
Gavin and Theo got in trouble at American football practice and had to run laps as a consequence. Gavin, who runs at a rate of 2 laps per minute, had completed 3 laps already when he was joined on the track by Theo. Theo’s pace is 3 laps per minute. At some point, the two will have run the same distance.
How long will that take?
Write simultaneous equations, graph them, and type the solution.
____ Minutes
Start by writing simultaneous equations. Let x=minutes and y=laps.
y=2x+3
y=3x
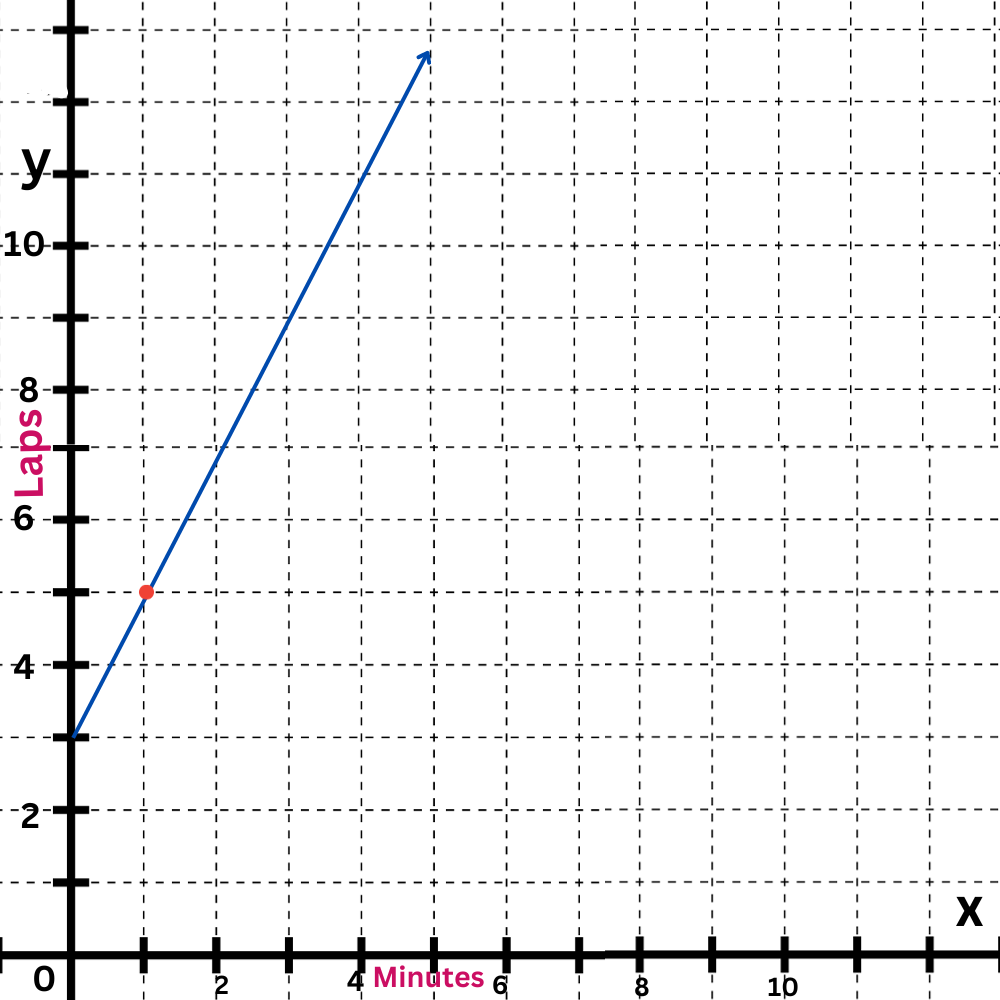
The first equation is y=2x+3.
The y-intercept is 3. Plot the point (0,3).
The slope is 2. Move up 2 and right 1 to find another point on the line.
Draw a line connecting them.
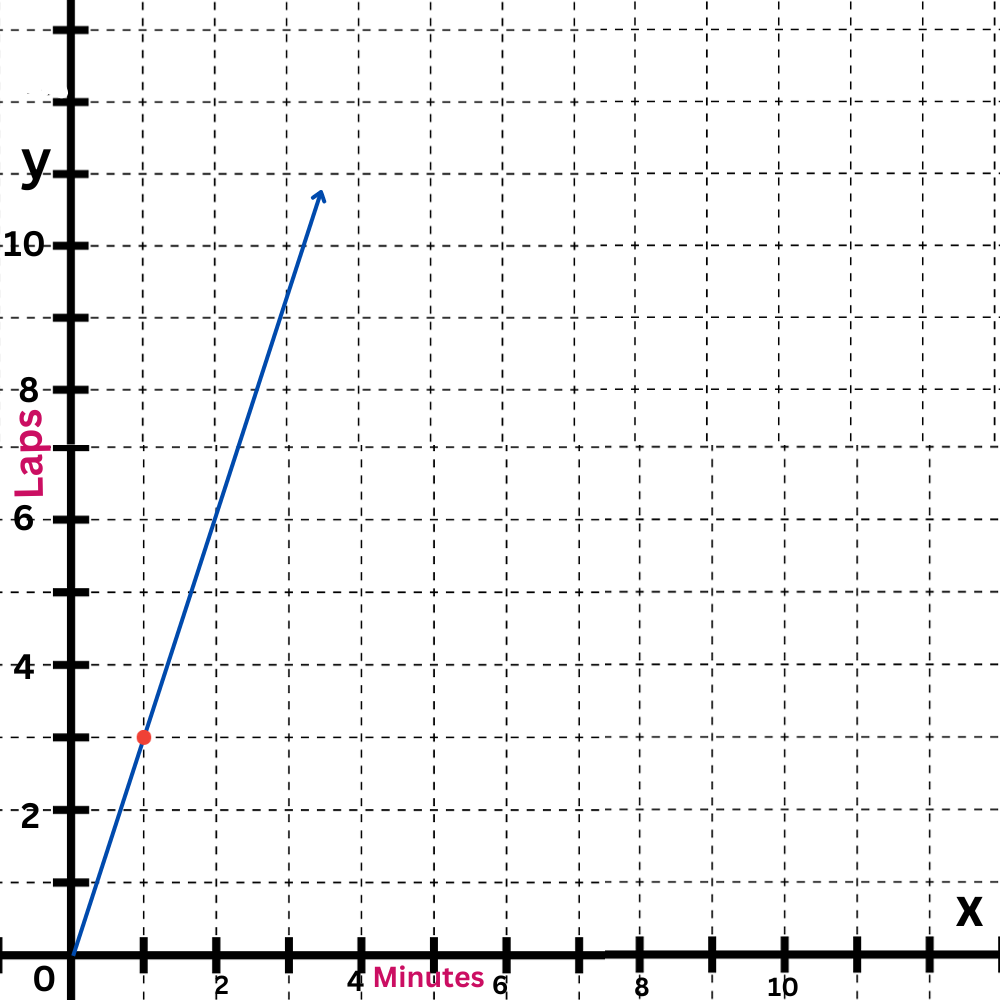
The second equation is y=3x.
The y-intercept is 0. Plot the point (0,0).
The slope is 3. Move up 3 and right 1 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
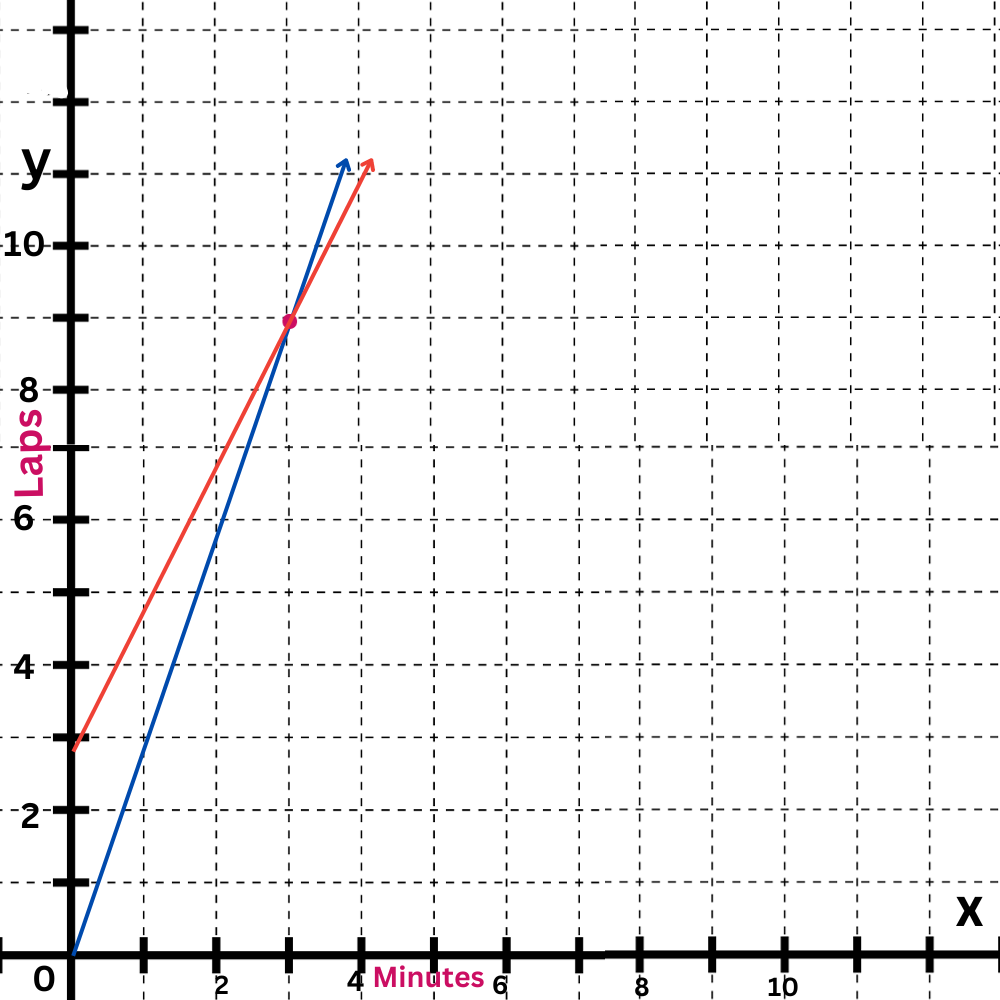
The lines intersect at (3,9).
After 3 minutes, Gavin and Theo will each have run 9 laps.

