Solve a pair of equations by graphing
key notes:
Solving systems of linear equations:
You can solve systems of equations in a few different ways.
Graphing:
You can solve systems of equations by graphing. Look for the point where the lines intersect.
Let’s try it! Solve the system of linear equations.
- y=3x+7
- y=–4x
Start by graphing the first equation, y=3x+7. Since this equation is in slope-intercept form, you can graph the line by plotting the y-intercept, 7, and then using the slope, 3.
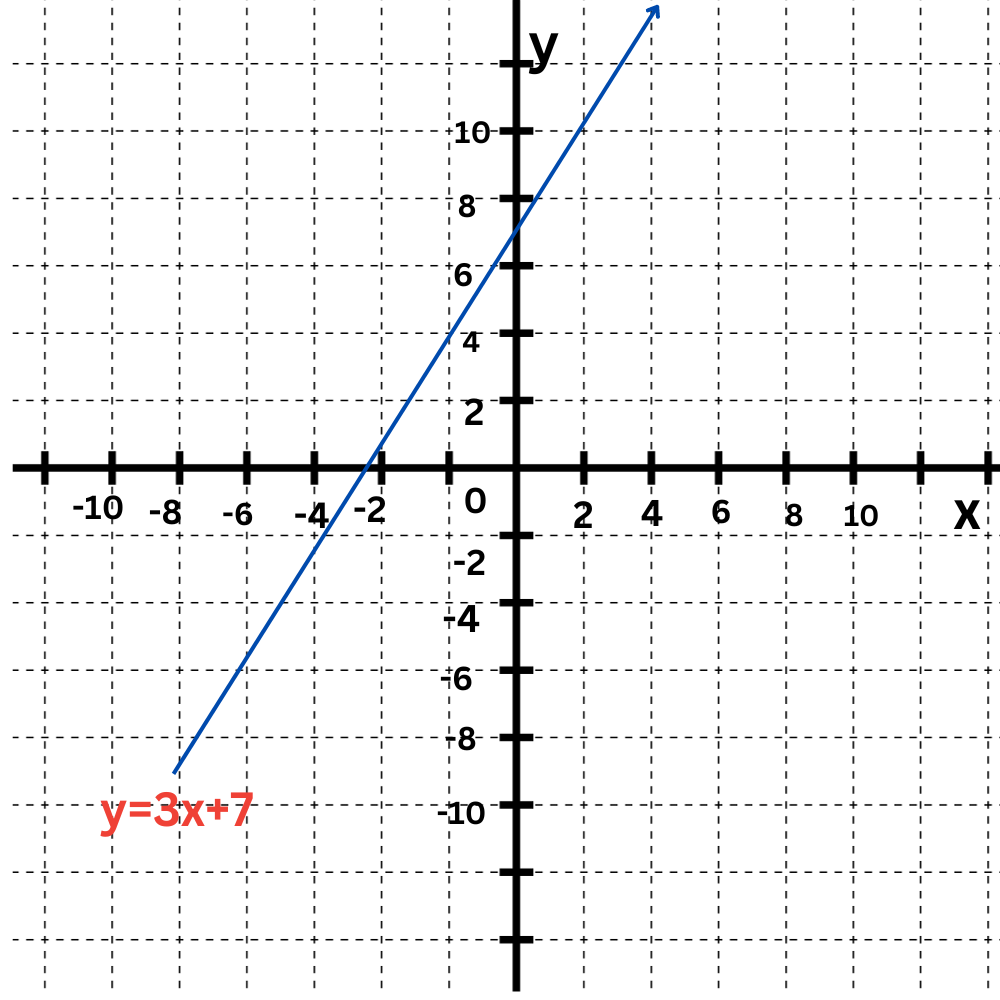
Now, graph the second equation, y=–4x, on the same coordinate plane. You can graph the line by plotting the y-intercept, 0, and then using the slope, –4.
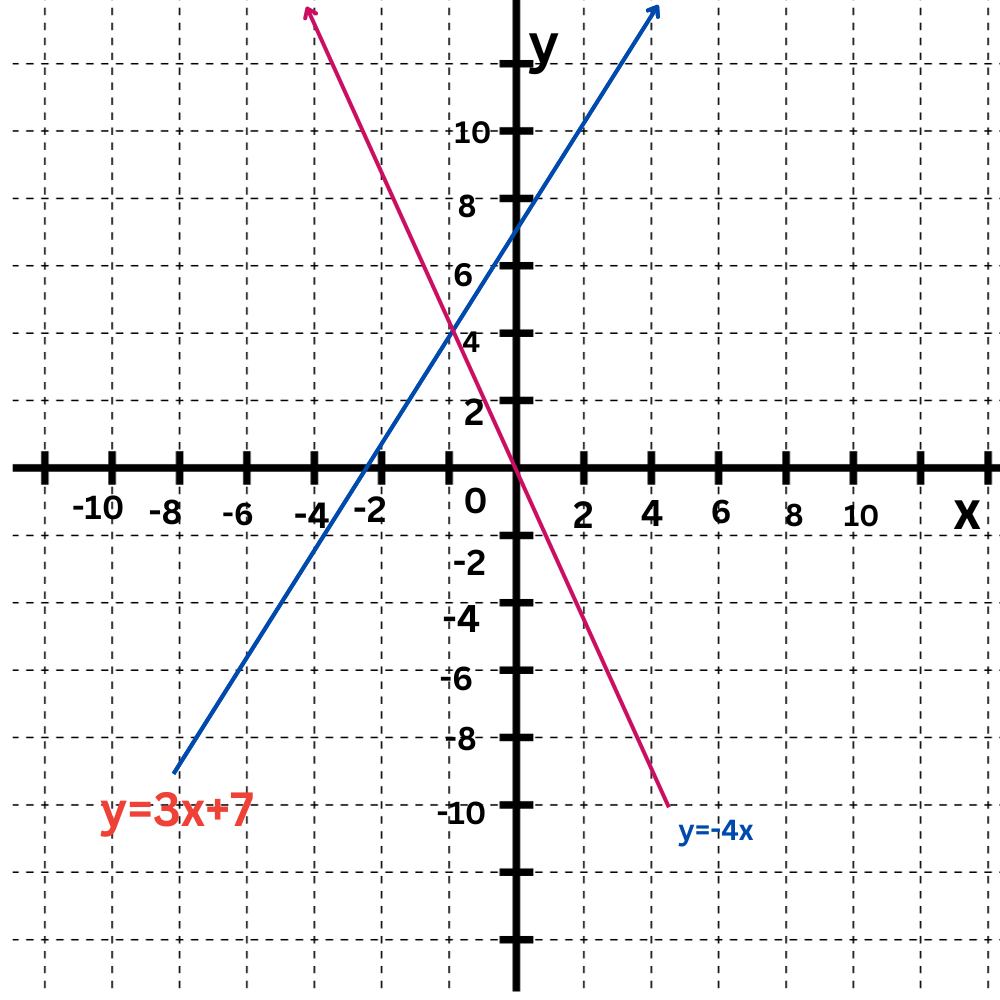
Last, find the point where the lines intersect.
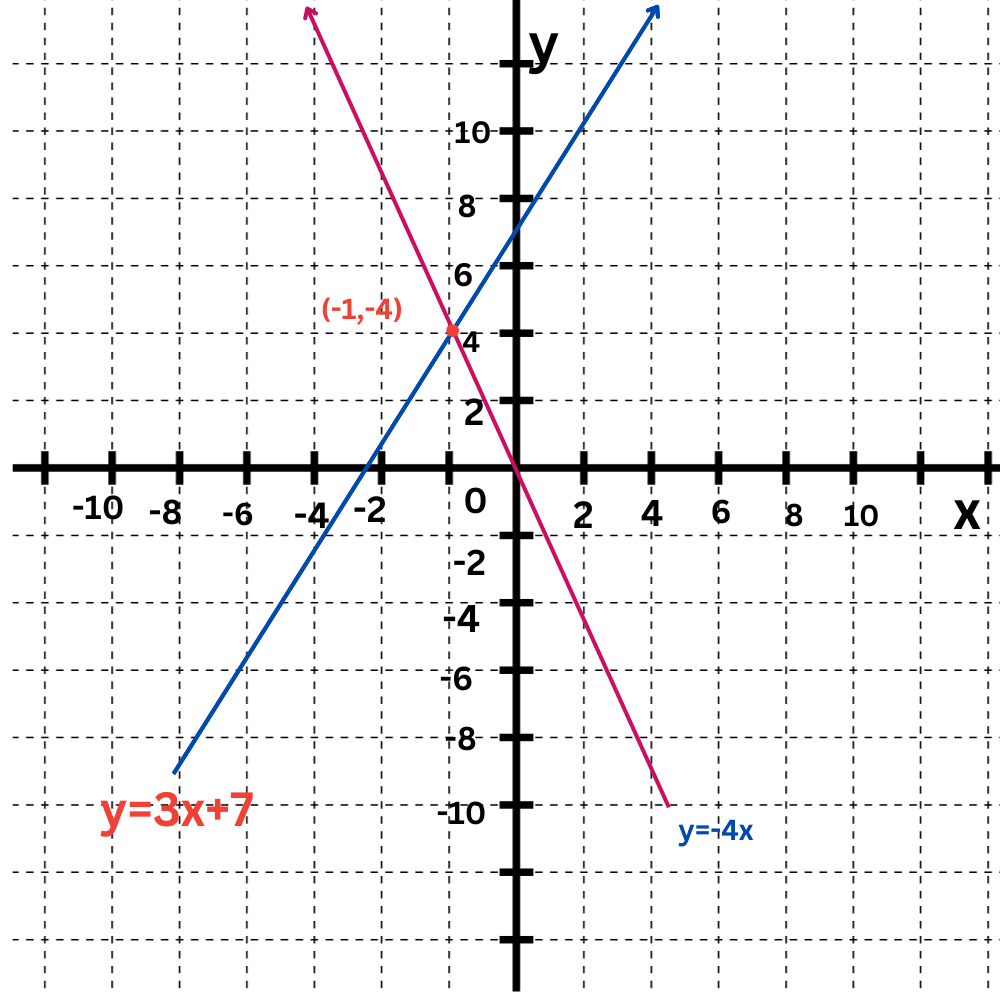
So, the solution to this system of equations is (–1,4).
You can check that this answer is correct by substituting –1 for x and 4 for y into the original equations.
- y=3x+7
- 4=3(–1)+7
- 4=–3+7
- 4=4
- y=–4x
- 4=–4(–1)
- 4=4
Since both equations are true, (–1,4) is the solution to the system of equations.
Learn with an example
Solve these simultaneous equations by graphing.
First graph the equations, and then type the solution.
y=2x+3
y=x
Click to select points on the graph.
The solution is ( ____, _____ ).
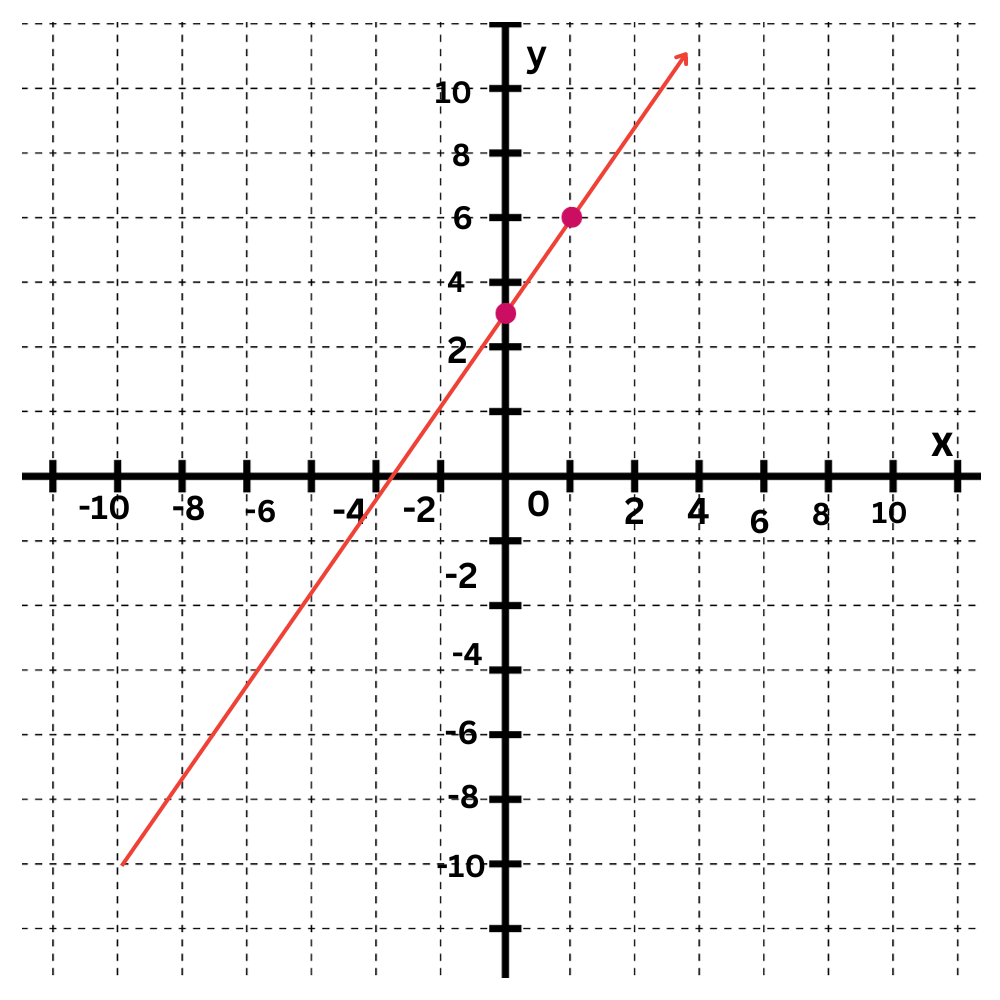
The first equation is y=2x+3.
The y-intercept is 3. Plot the point (0,3).
The slope is 2. Move up 2 and right 1 to find another point on the line.
Draw a line connecting them.
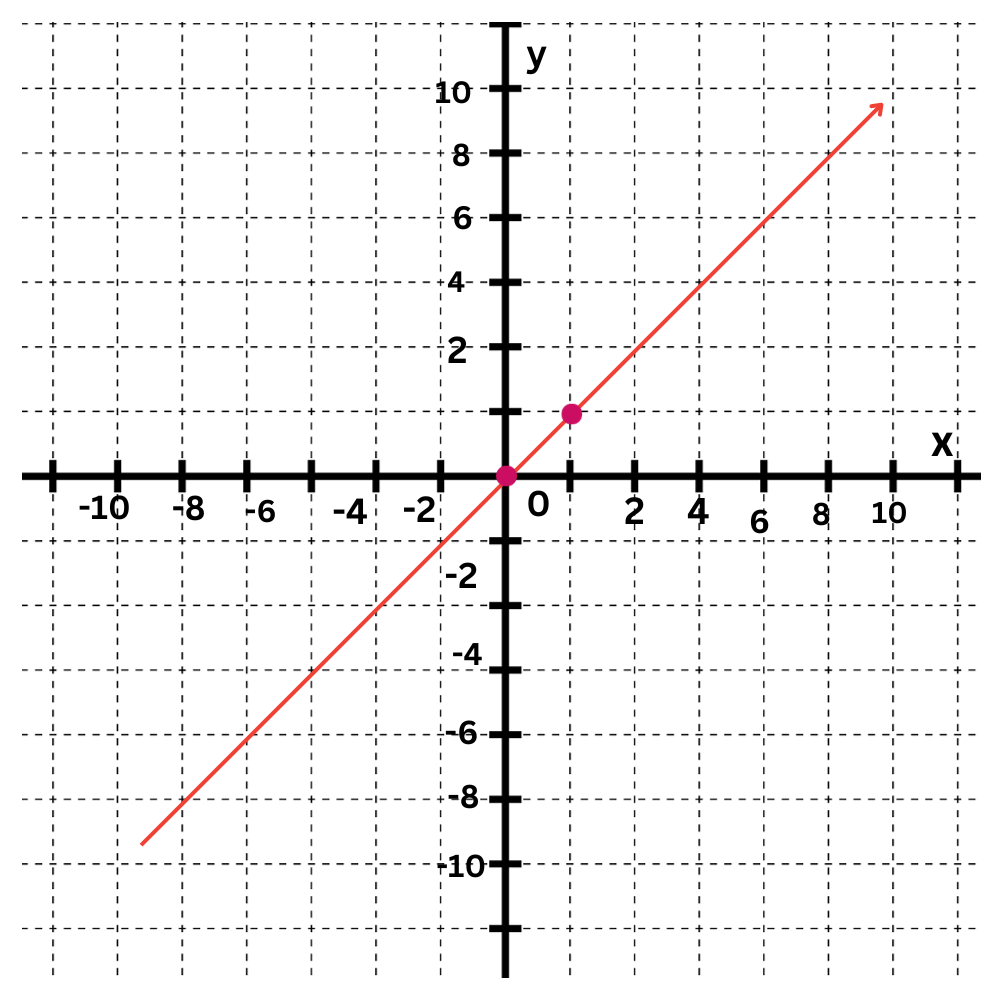
The second equation is y=x.
The y-intercept is 0. Plot the point (0,0).
The slope is 1. Move up 1 and right 1 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
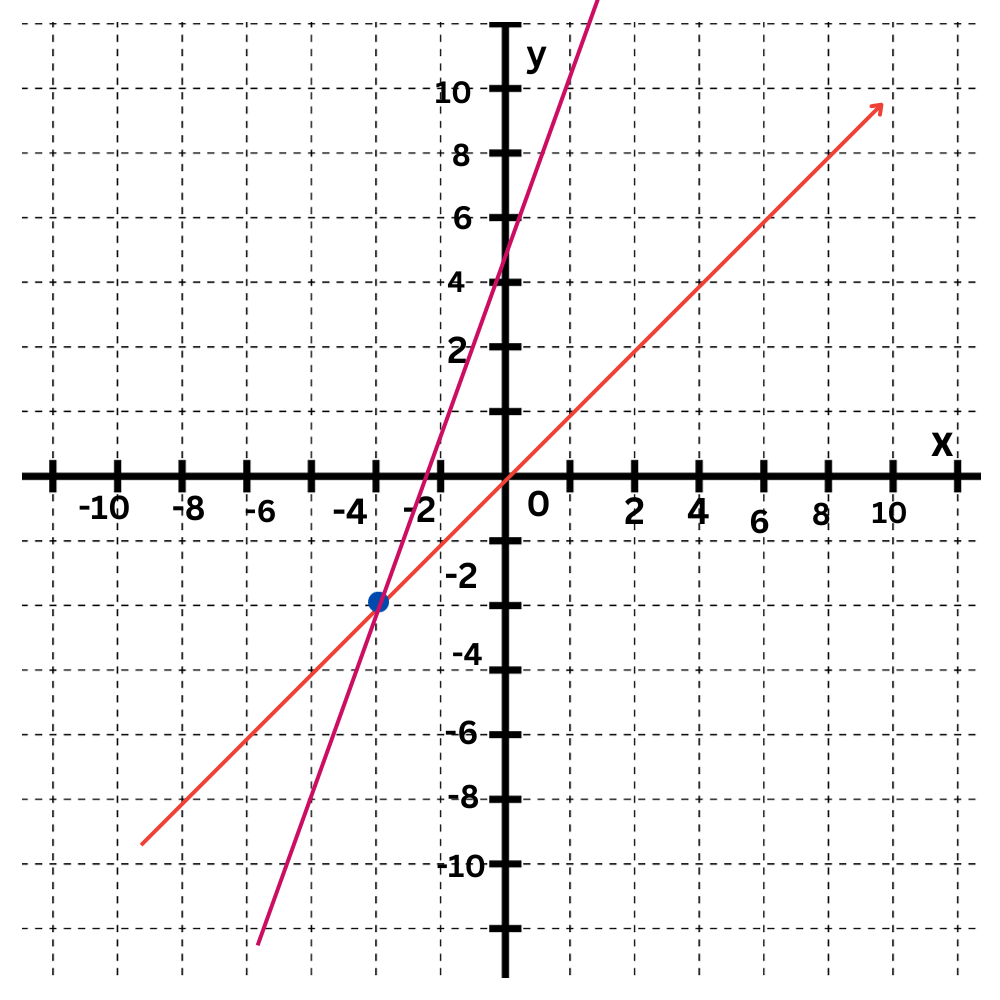
The lines intersect at (–3,–3), so the solution to the simultaneous equations is (–3,–3).
Solve these simultaneous equations by graphing.
First graph the equations, and then type the solution.
y=2x–1
y=x+2
Click to select points on the graph.
The solution is ( ____, _____ ).
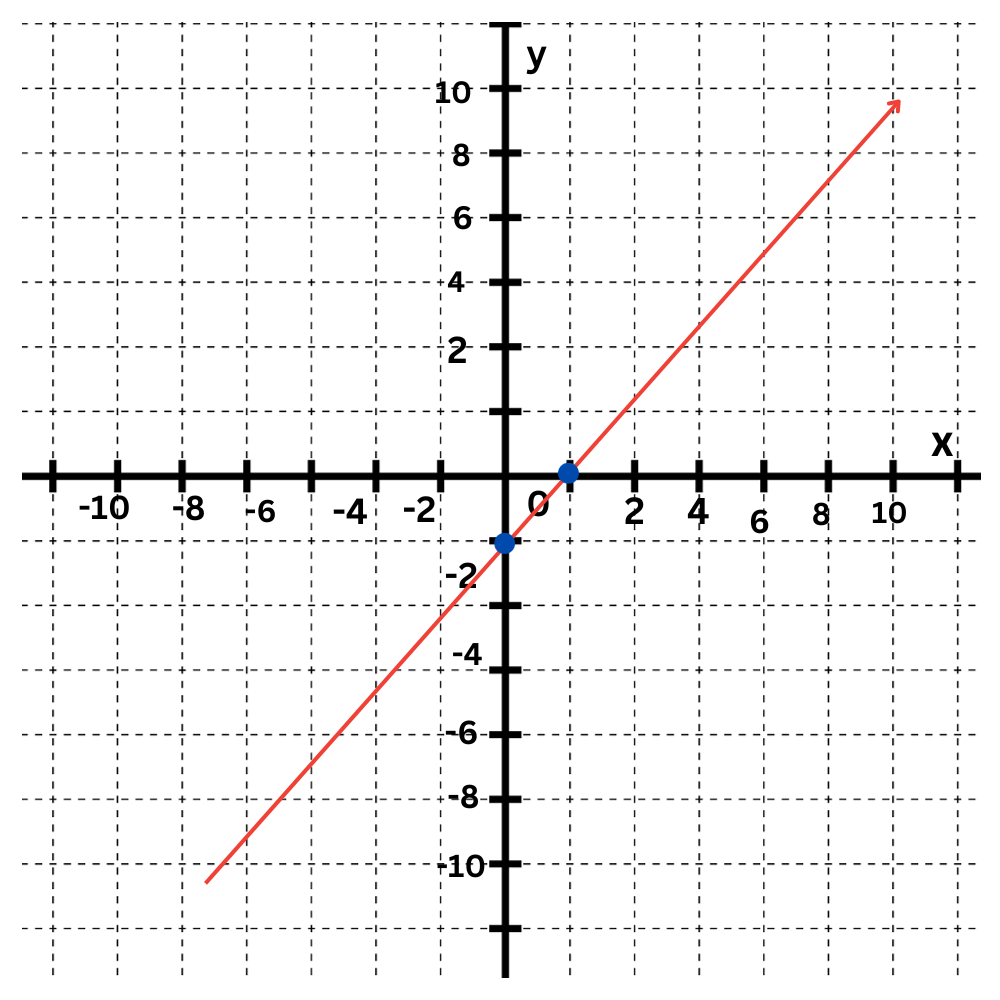
The first equation is y=2x–1.
The y-intercept is–1Plot the point (0,–1).
The slope is 2. Move up 2 and right 1 to find another point on the line.
Draw a line connecting them.
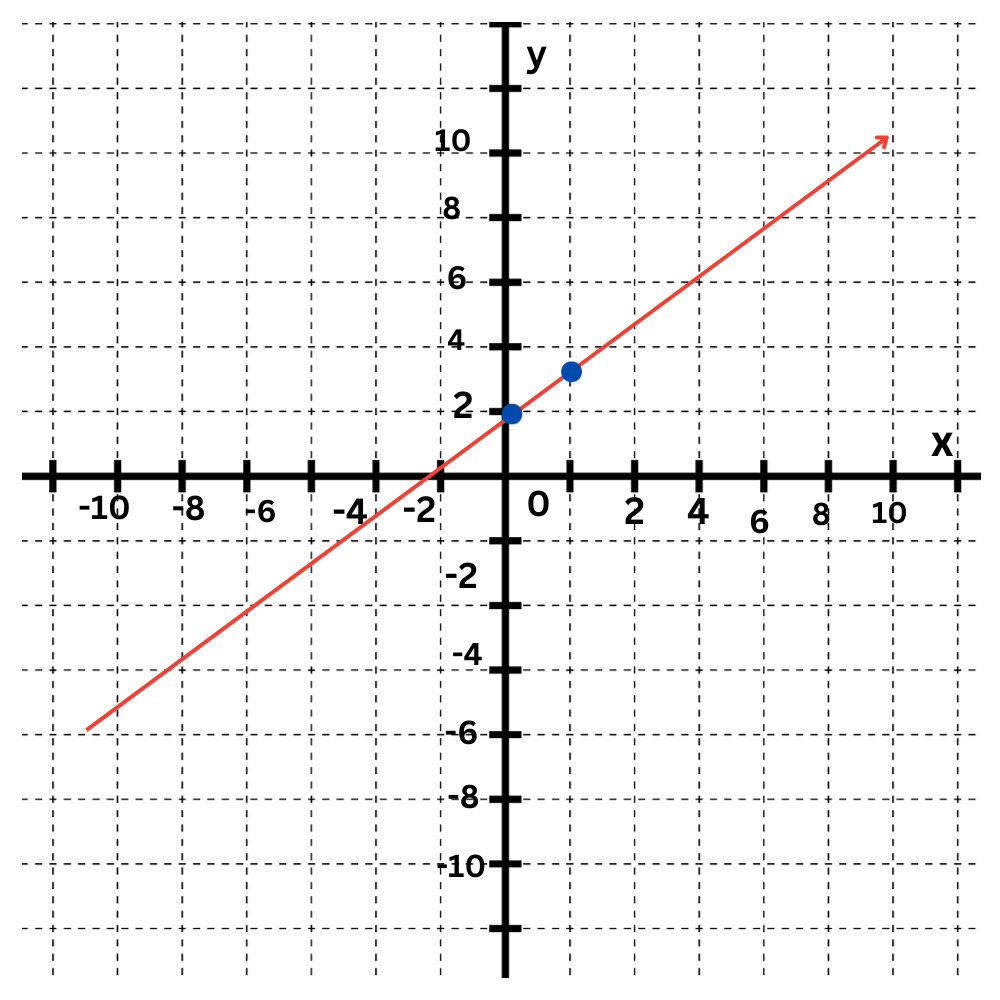
The second equation is y=x+2.
The y-intercept is 2. Plot the point (0,2).
The slope is 1. Move up 1 and right 1 to find another point on the line.
Draw a line connecting them.
Finally, identify the point of intersection.
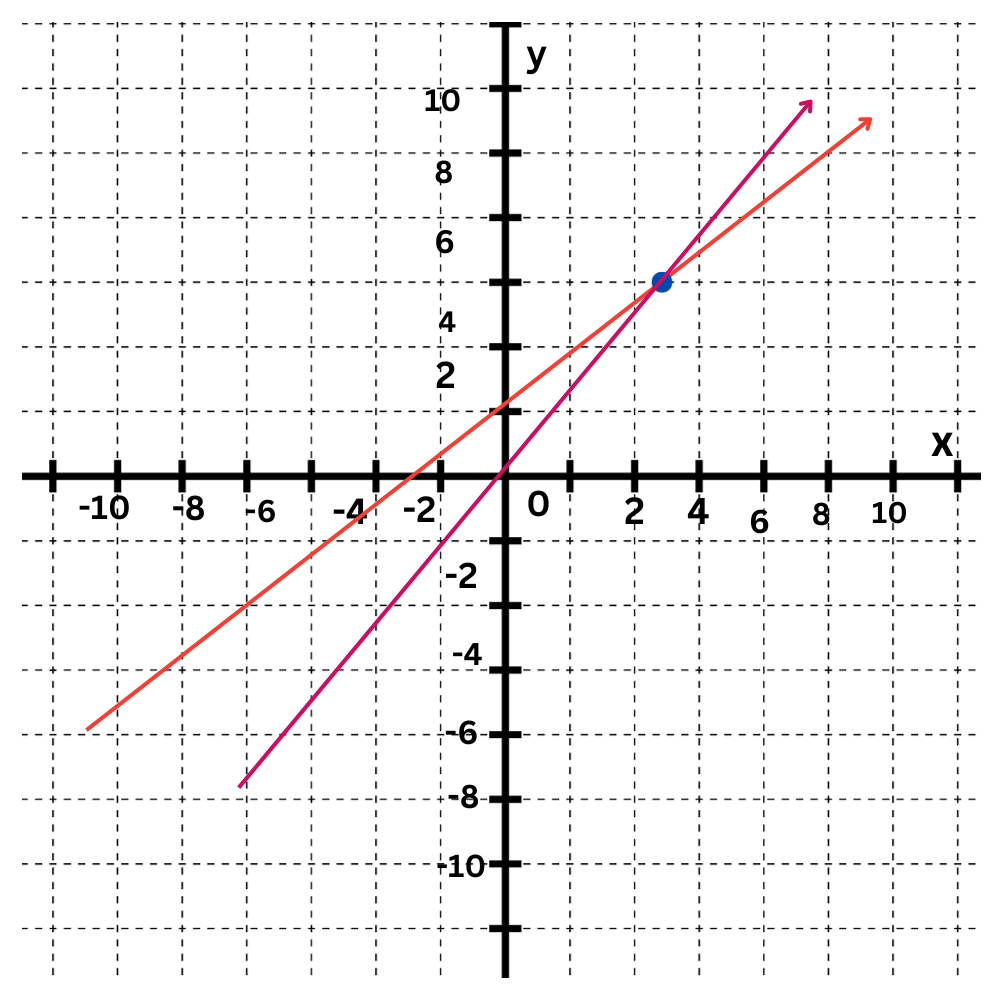
The lines intersect at (3,5), so the solution to the simultaneous equations is (3,5).

