Find the distance between two parallel lines
key notes:
The distance between two parallel lines is the distance between one line and a point on the other line.
The distance between a point and a line is the length of the segment perpendicular to the line from the point.
Learn with an example
Line ℓ1 has the equation y=–4 and line ℓ2 has the equation y=5.
Find the distance between ℓ1 and ℓ2.
The line ℓ1 is a horizontal line with a y-intercept of –4. The line ℓ2 is a horizontal line with a y-intercept of 5. Since ℓ1 and ℓ2 are both horizontal lines with different y-intercepts, they are parallel.
To find the distance between ℓ1 and ℓ2, pick a point on one of the lines and find the distance from that point to the other line. For convenience, pick the y-intercept of ℓ1, (0,–4). Call this point R.
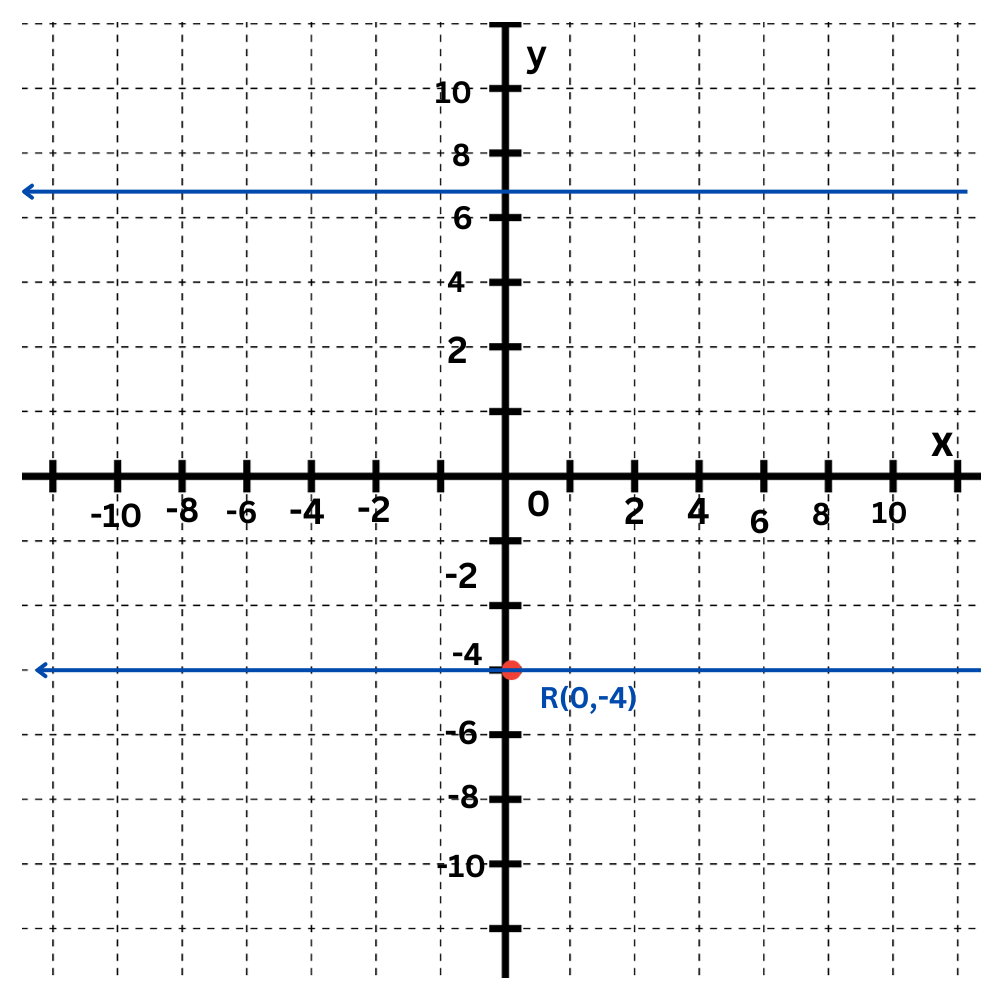
Now, calculate the distance between ℓ2 and R. The point S(0,5) lies on ℓ2 and is directly above R.
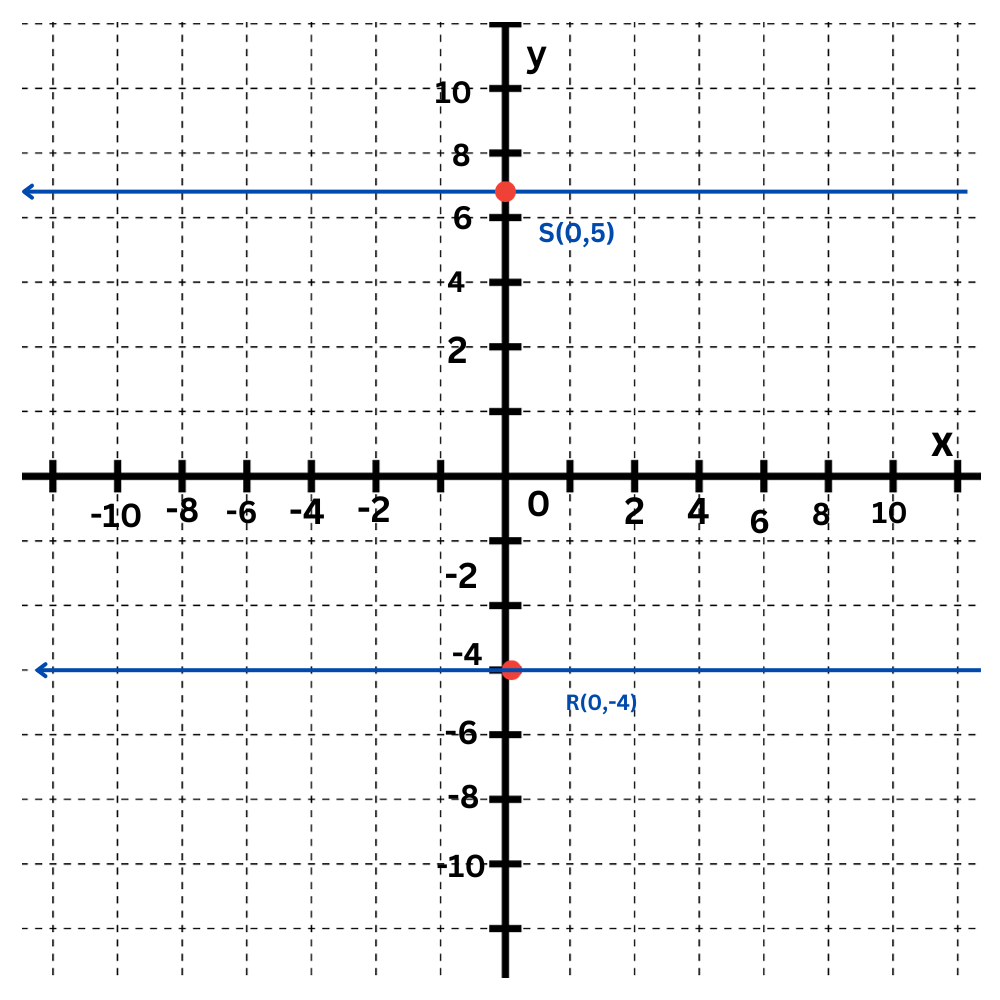
The segment perpendicular to ℓ2 from R is the vertical segment between S and R, which is RS.
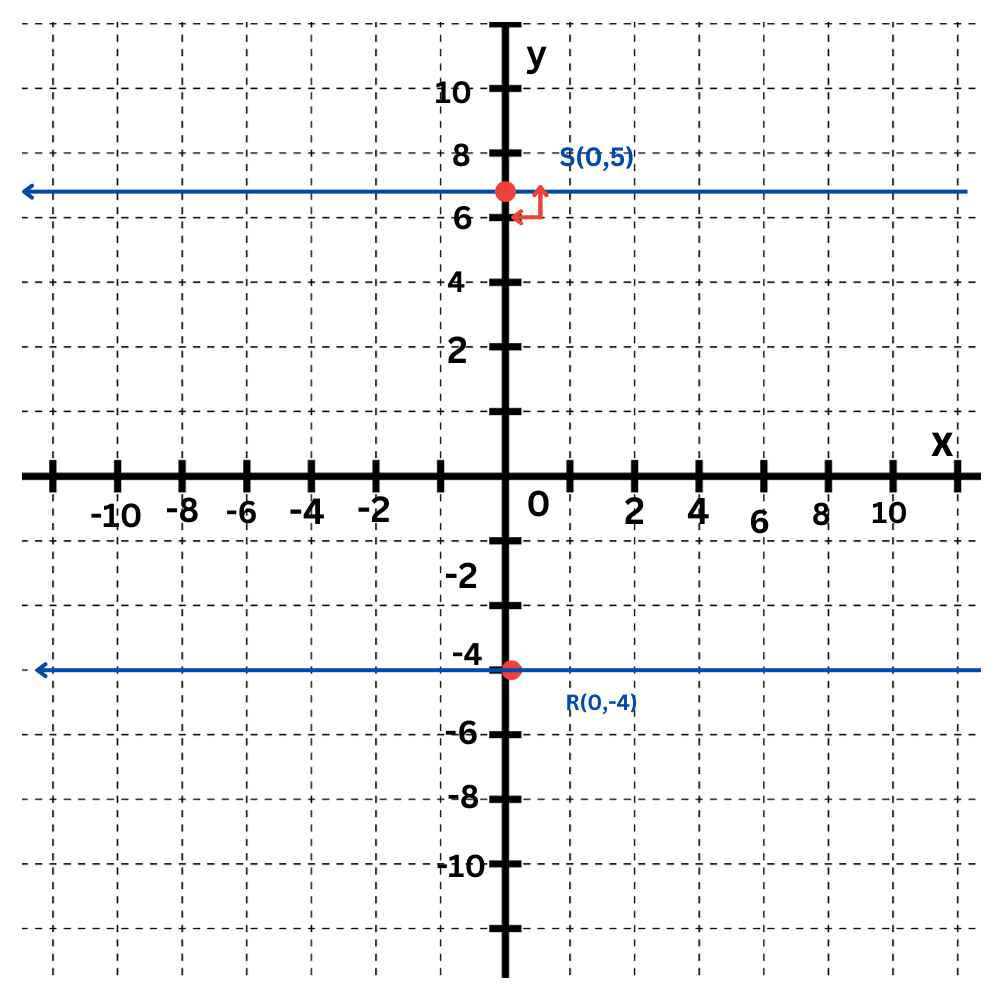
To find the distance between ℓ1 and ℓ2, find the length of RS. The length is the absolute value of the difference in y-coordinates of S and R, which is |5––4|=9. So, the distance between ℓ1 and ℓ2 is 9.
Line ℓ1 has the equation y=–3 and line ℓ2 has the equation y=7.
Find the distance between ℓ1 and ℓ2.
To find the distance between ℓ1 and ℓ2, find the length of TU. The length is the absolute value of the difference in y-coordinates of U and T, which is |7––3|=10. So, the distance between ℓ1 and ℓ2 is 10.
Line ℓ1 has the equation y=–5 and line ℓ2 has the equation y=–3.
Find the distance between ℓ1 and ℓ2.
To find the distance between ℓ1 and ℓ2, find the length of BC. The length is the absolute value of the difference in y-coordinates of C and B, which is |–3––5|=2. So, the distance between ℓ1 and ℓ2 is 2.
let’s practice:

