Find the distance between a point and a line
key notes:
The distance between a point and a line is the length of the segment perpendicular to the line from the point.
Learn with an example
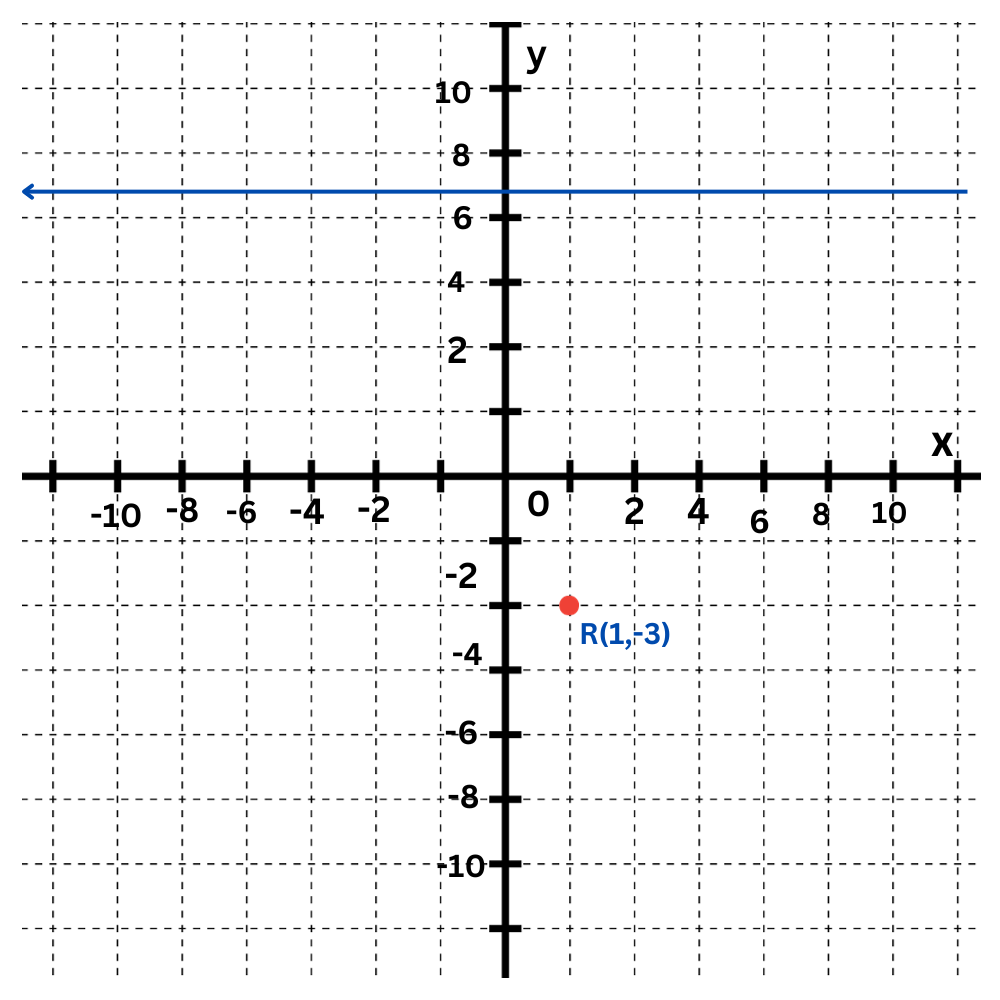
Line ℓ has equation y=7.
Find the distance between ℓ and the point R(1,–3).
The line ℓ is a horizontal line with a y-intercept of 7. The point R has an x-coordinate of 1 and a y-coordinate of –3.
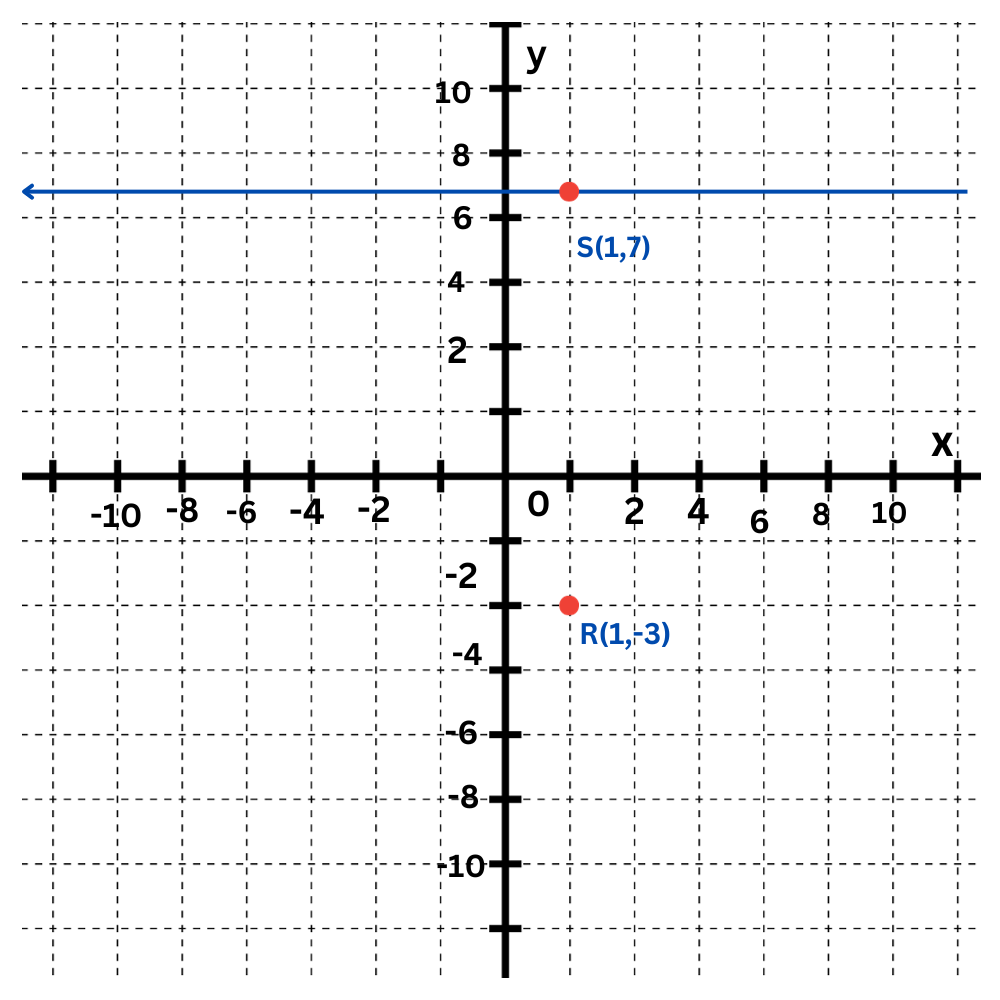
Look for the point on ℓ that is directly above R. This point is S(1,7).
The segment perpendicular to ℓ from R is the vertical segment between S and R, which is RS.
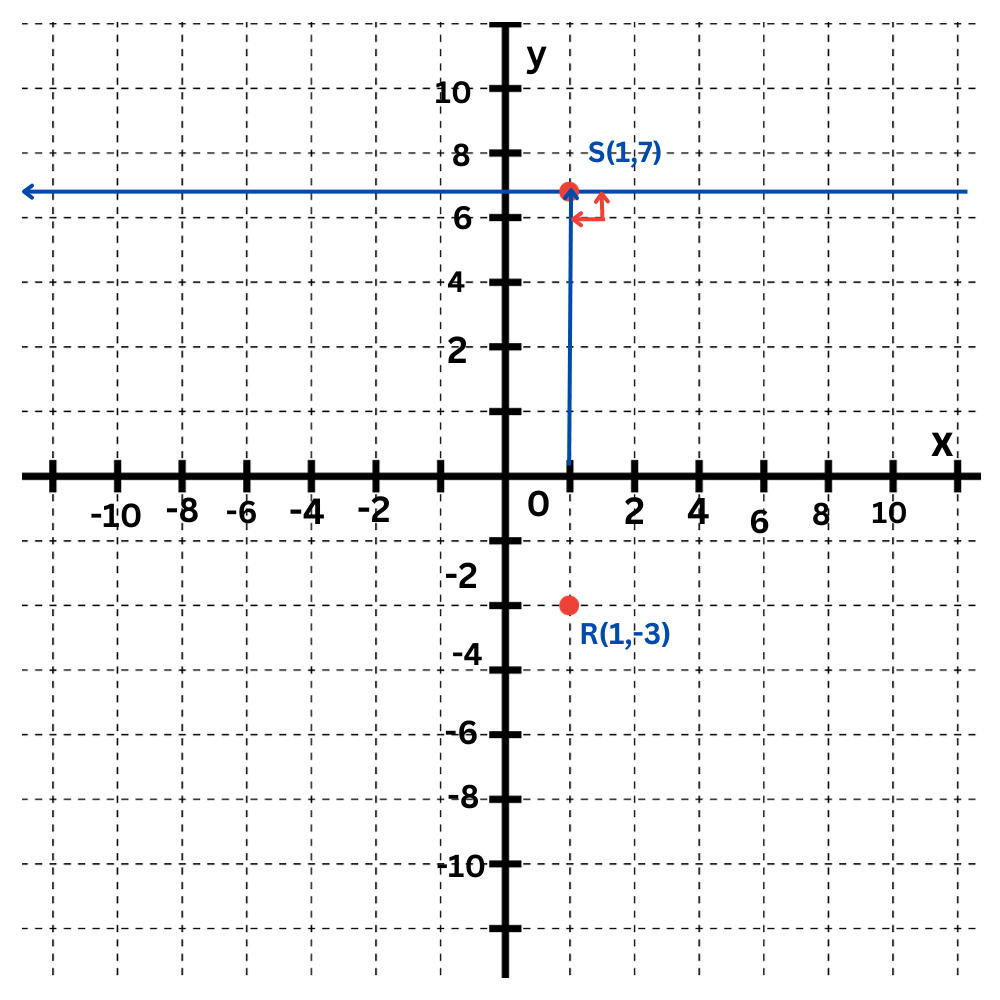
To find the distance between ℓ and R, find the length of RS. The length is the absolute value of the difference in y-coordinates of S and R, which is |7– –3|=10.
So, the distance between ℓ and R is 10.
Line ℓ has equation y=5.
Find the distance between ℓ and the point D(–5,–7).
Round your answer to the nearest tenth.
The line ℓ is a horizontal line with a y-intercept of 5. The point D has an x-coordinate of–5 and a y-coordinate of –7.
Look for the point on ℓ that is directly above D. This point is E(–5,5).
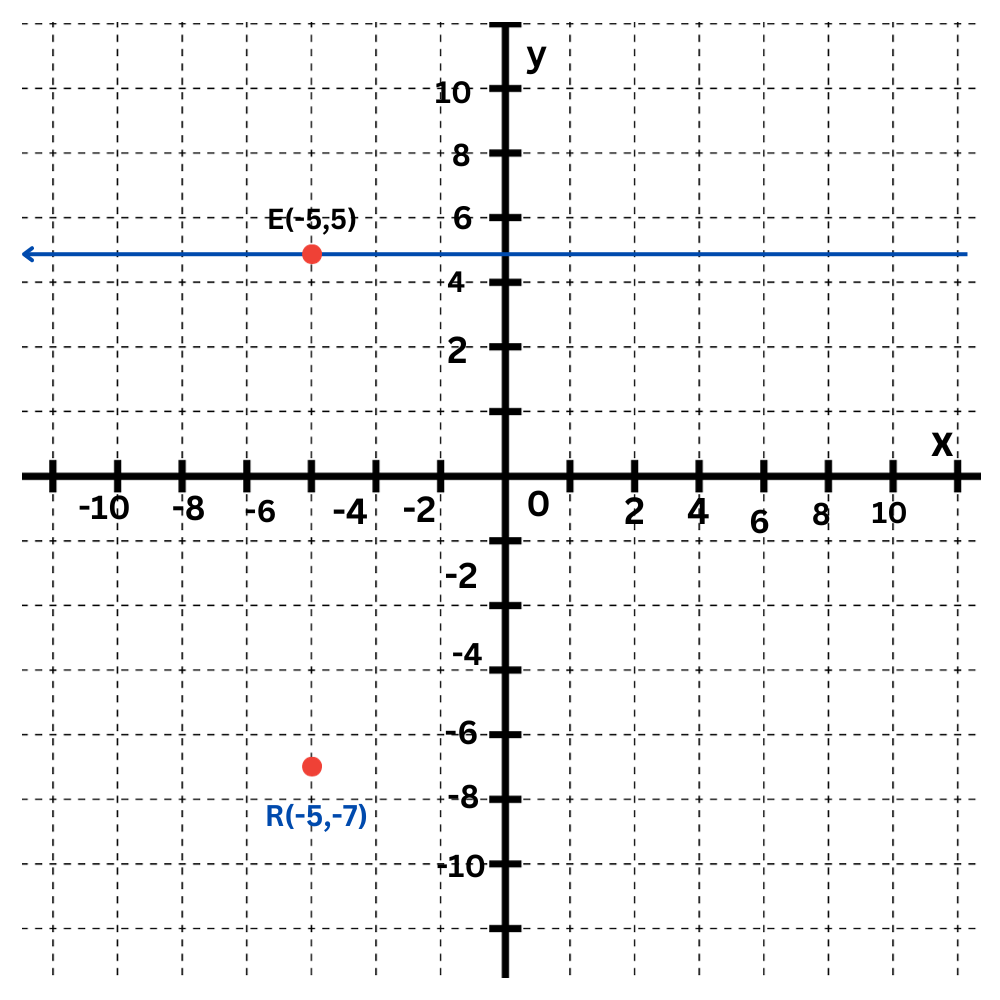
The segment perpendicular to ℓ from D is the vertical segment between E and D, which is DE.
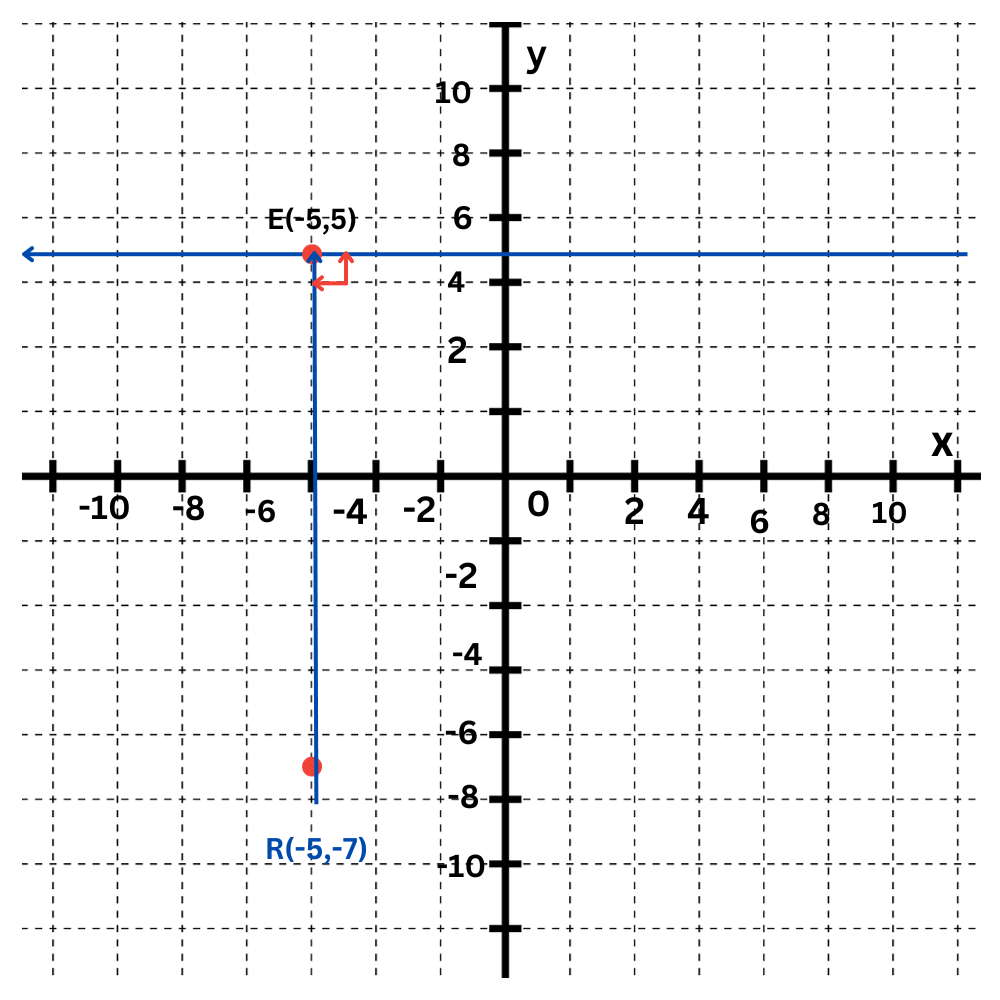
To find the distance between ℓ and D, find the length of DE. The length is the absolute value of the difference in y coordinates of E and D, which is |5 – -7|=12. so the distance
let’s practice:

