Multiply and divide rational numbers
key notes:
Multiplying Rational Numbers
- Definition:
- To multiply two rational numbers, multiply the numerators together and the denominators together.
- Formula
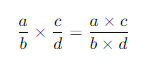
- Steps:
- Multiply the numerators: a×c
- Multiply the denominators: b×d
- Simplify the resulting fraction, if possible.
- Example:
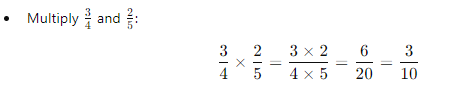
- Multiplying by a Whole Number:
- When multiplying a rational number by a whole number, treat the whole number as a fraction with denominator 1.
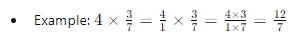
Dividing Rational Numbers
- Definition:
- To divide two rational numbers, multiply the first rational number by the reciprocal of the second rational number.
- Formula:

- Steps:
- Find the reciprocal of the divisor (flip the numerator and the denominator of the second fraction).
- Multiply the first fraction by this reciprocal.
- Simplify the resulting fraction, if possible.
- Example:
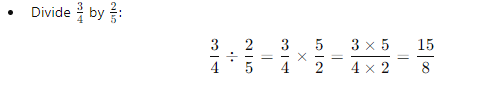
- Dividing by a Whole Number:
- When dividing a rational number by a whole number, treat the whole number as a fraction with denominator 1 and then find its reciprocal.
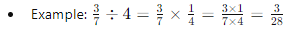
Simplifying Rational Numbers
- After multiplying or dividing rational numbers, always simplify the resulting fraction by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by this number.Example:

Practice Problems
- Multiplying Rational Numbers:
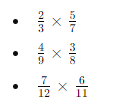
- Dividing Rational Numbers:
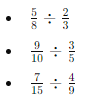
- Mixed Practice:
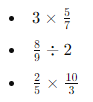
Tips for Success
- Reciprocals:
- Remember to find the reciprocal when dividing by a fraction.
- Simplifying:
- Always simplify your answer to its lowest terms.
- Multiplication and Division Rules:
- Use the multiplication rule for both operations: multiply the numerators together and the denominators together for multiplication, and multiply by the reciprocal for division.
- Check Your Work:
- Double-check your multiplication and division to avoid small mistakes.
Learn with an example
🔮 Divide.
1/10 ÷ 1/2 =
Turn this from a division problem into a multiplication problem by multiplying by the reciprocal.
1/10 ÷ 1/2 = 1/10 x 2/1
Cancel common factors, then multiply.
1/10 x 2/1 = 1/5 x 1/1
= 1 x 1 / 5 x 1
= 1/5
🔮 Divide.
1/4 ÷ 1/2 =
Turn this from a division problem into a multiplication problem by multiplying by the reciprocal.
1/4 ÷ 1/2 = 1/4 x 2/1
Cancel common factors, then multiply.
1/4 x 2/1 = 1/2 x 1/1
= 1 x 1 / 2 x 1
= 1/2
🔮 Divide.
1/8 ÷ 1/6 =
Turn this from a division problem into a multiplication problem by multiplying by the reciprocal.
1/8 ÷ 1/6 = 1/8 x 6/1
Cancel common factors, then multiply.
1/8 x 6/1 = 1/4 x 3/1
= 1 x 3 / 4 x 1
= 3/4
Let’s Practice!

