Add, subtract, multiply, and divide integers
key notes:
Adding Integers
- Rules:
- Same Signs: Add the absolute values and keep the sign.
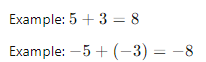
- Different Signs: Subtract the smaller absolute value from the larger absolute value and keep the sign of the number with the larger absolute value.
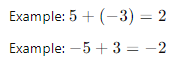
- Number Line:
- To add integers on a number line, start at the first number and move to the right for positive integers and to the left for negative integers.
Subtracting Integers
- Rules:
- Subtracting an Integer: To subtract an integer, add its opposite.
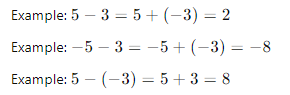
- Number Line:
- To subtract integers on a number line, start at the first number and move to the left for positive subtractions and to the right for negative subtractions.
Multiplying Integers
- Rules:
- Same Signs: The product of two integers with the same sign is positive.
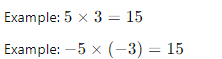
- Different Signs: The product of two integers with different signs is negative.
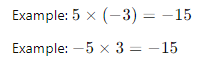
- Examples:
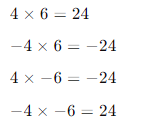
Dividing Integers
- Rules:
- Same Signs: The quotient of two integers with the same sign is positive.
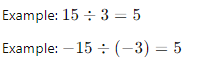
- Different Signs: The quotient of two integers with different signs is negative.
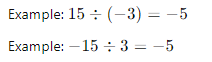
- Examples:
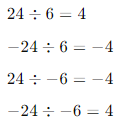
Tips for Students
- Consistent Practice:
- Regular practice with varied problems helps reinforce the rules and concepts.
- Use of Number Lines:
- Number lines are particularly helpful for visualizing addition and subtraction of integers.
- Understanding Signs:
- Focus on the rules regarding the signs of integers to avoid common mistakes.
Classroom Activities
- Interactive Number Line:
- Create a large number line on the classroom floor. Have students physically walk the number line to add or subtract integers.
- Integer Card Games:
- Use cards with positive and negative integers. Students draw cards and practice addition, subtraction, multiplication, and division.
- Worksheets:
- Provide worksheets with mixed integer operations to solve, ensuring varied practice.
- Group Activities:
- Have students work in groups to solve integer problems, fostering collaboration and discussion.
Learn with an example
When you add a positive number and a negative number:
- If the positive number has a bigger magnitude, the result is positive.
- If the negative number has a bigger magnitude, the result is negative.
Ex:
When you add a positive number, 4,854,093, and a negative number, –650,163, the result has the same sign as the number with the larger magnitude.
The magnitude of 4,854,093 is 4,854,093.
The magnitude of -650,163 is 650,163.
Since 4,854,093 has a larger magnitude and 4,854,093 is positive, the result is positive.
You can check your answer by doing the maths.
4,854,093 + -650,163 = 4,203,930
As you can see, the result is positive.
When you add negative numbers, the result is negative.
Ex:
When you add two negative numbers, like –17 and –46,337, the result is negative.
You can check your answer by doing the maths.
-17 + -46,337 = -46,354
As you can see, the result is negative.
Instead of subtracting a number, you can add its opposite.
When you add a positive number and a negative number:
- If the positive number has a bigger magnitude, the result is positive.
- If the negative number has a bigger magnitude, the result is negative.
Ex:
Since you are subtracting a negative number, add a positive number instead:
-291 − –9 = -291 + 9
Now you have a negative number, –291, and a positive number, 9. The result has the same sign as the number with the larger magnitude.
The magnitude of -291 is 291.
The magnitude of 9 is 9.
The result is negative since -291 has a larger magnitude and -291 is negative.
You can check your answer by doing the maths.
-291 − -9 = -282
As you can see, the result is negative
Is 222 + -5,827 positive or negative?
- positive
- negative
When you add a positive number, 222, and a negative number, -5,827, the result has the same sign as the number with the larger magnitude.
The magnitude of 222 is 222.
The magnitude of -5,827 is 5,827.
Since -5,827 has a larger magnitude and -5,827 is negative, the result is negative.
You can check your answer by doing the maths.
222 + -5,827 = -5,605
As you can see, the result is negative.
Let’s Practice!

