Construct the inscribed or circumscribed circle of a triangle
Key Notes:
The circumcenter of a triangle is the centre of its circumscribed circle. It is equidistant from all three vertices, and it is the intersection of the perpendicular bisectors of each of the triangle’s sides.
To construct the circumcenter, it is sufficient to find the intersection of two perpendicular bisectors, since the third perpendicular bisector will also pass through this point.
Learn with an example
D is the circumcenter of △ABC. Construct the circumscribed circle of △ABC.
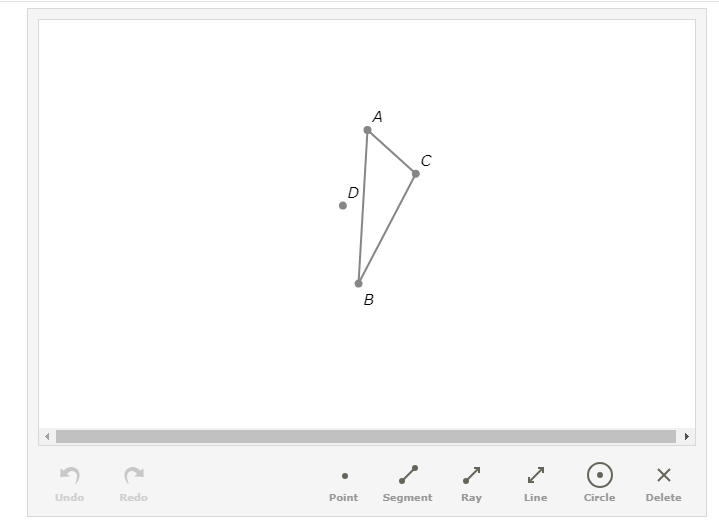
To construct the circumscribed circle of △ABC, carry out the following step:
Draw a circle with radius BD centred at D.
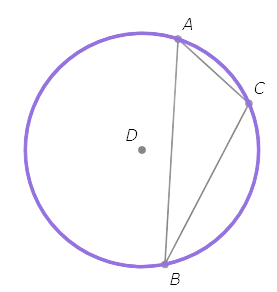
The circumcenter D is the centre of the circumscribed circle, and A is a point on the circumscribed circle, so ⨀D is the circumscribed circle of △ABC.
D is the circumcenter of △ABC. Construct the circumscribed circle of △ABC.
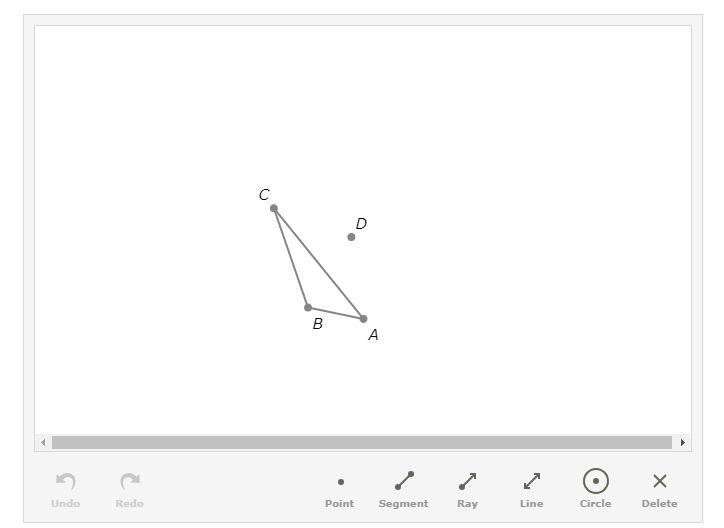
To construct the circumscribed circle of △ABC, carry out the following step:
Draw a circle with radius CD centred at D.

The circumcenter D is the centre of the circumscribed circle, and A is a point on the circumscribed circle, so ⨀D is the circumscribed circle of △ABC.
D is the circumcenter of △ABC. Construct the circumscribed circle of △ABC.
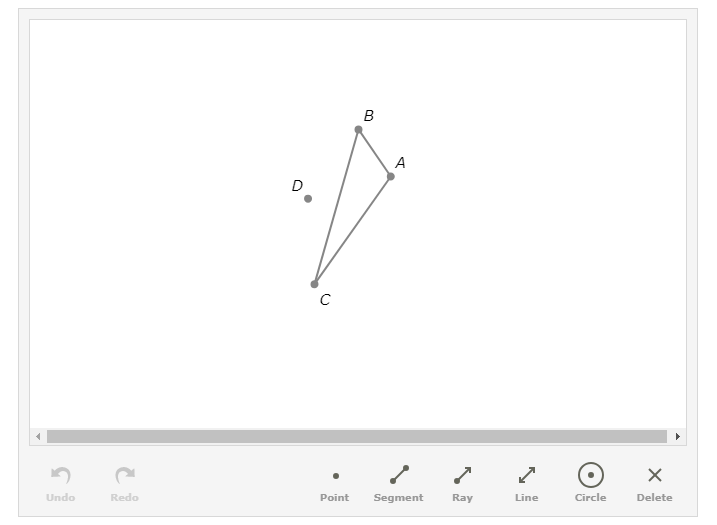
To construct the circumscribed circle of △ABC, carry out the following step:
Draw a circle with radius CD centred at D.

The circumcenter D is the centre of the circumscribed circle, and A is a point on the circumscribed circle, so ⨀D is the circumscribed circle of △ABC.
Let’s practice!🖊️

