Construct a regular hexagon inscribed in a circle
Learn with an example
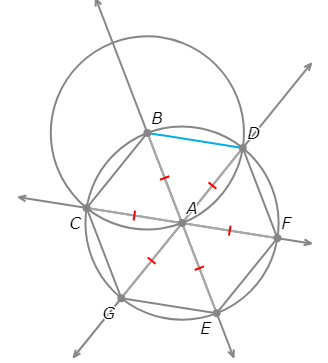
The diagram below shows a nearly completed construction of a regular hexagon inscribed in ⨀A with a vertex at B. Complete the construction.
Part of the construction was done for you. Here are the steps to create this part of the construction.
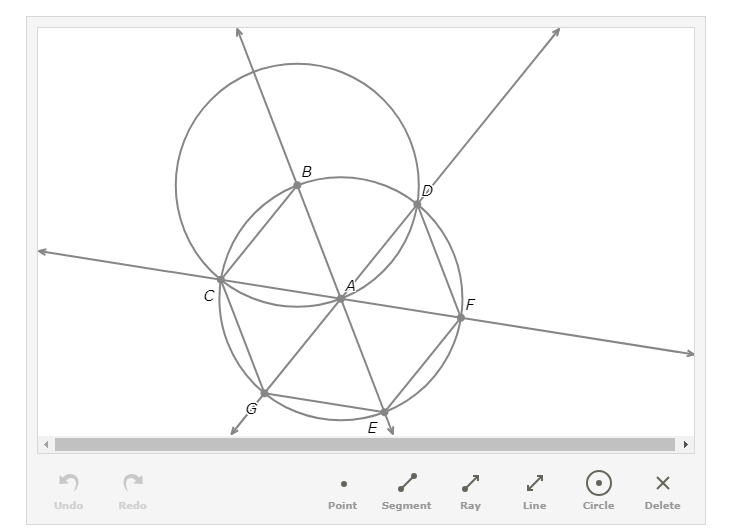
Start with the objects in the diagram below.
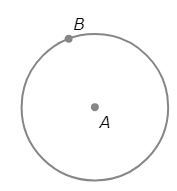
- Draw a circle with radius AB centred at B.
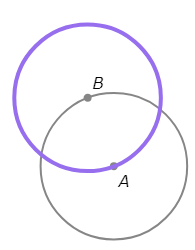
- Mark the points where ⨀A and ⨀B intersect. Call them C and D.
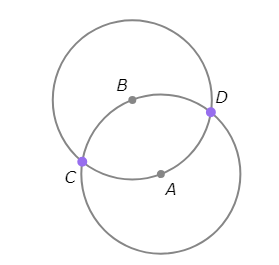
- Since A, C, and D are all on ⨀B, AB=BC=BD. Since B, C, and D are all on ⨀A, AB=AC=AD. This means that AB=AC=AD=BC=BD.
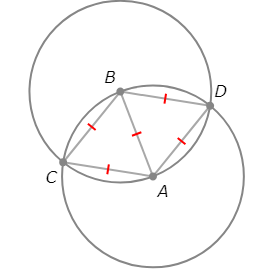
- So, △ABC and △ABD are congruent equilateral triangles.
- Draw the line through A and B.
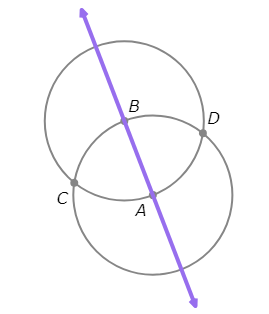
- Draw the line through A and C.
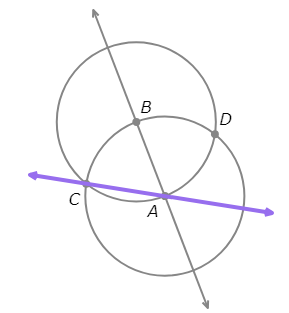
- Draw the line through A and D.
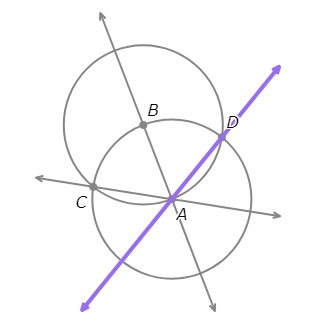
- Mark the point other than B where ⨀A and AB intersect. Call it E.

- Mark the point other than C where ⨀A and AC intersect. Call it F.
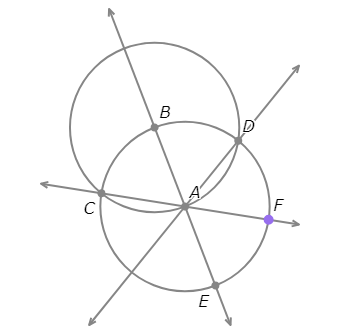
- Mark the point other than D where ⨀A and AD intersect. Call it G.
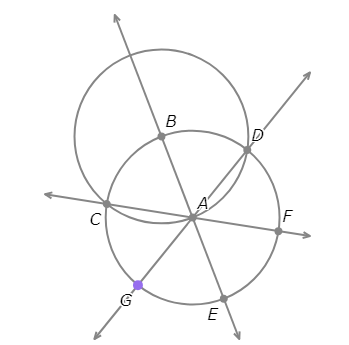
- Draw the segment between B and C.
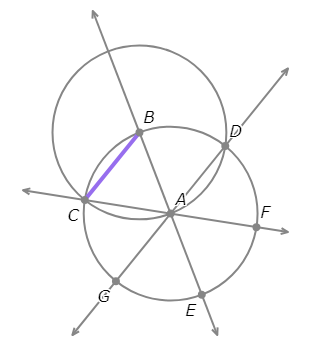
- Draw the segment between C and G.
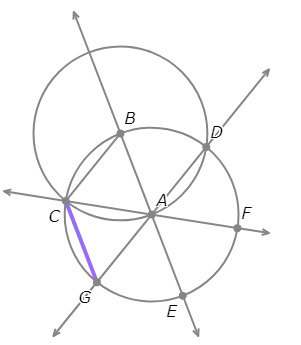
- Draw the segment between G and E.
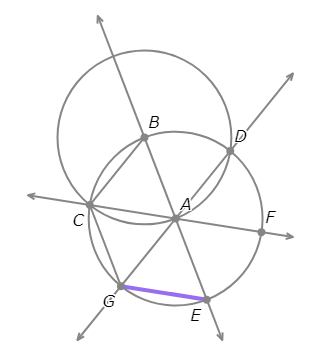
- Draw the segment between E and F.
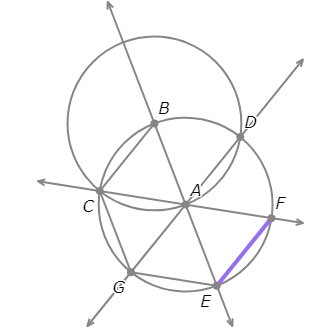
- Draw the segment between F and D.
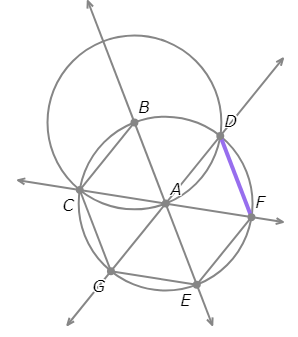
Complete the construction.
- To complete the construction of a regular hexagon inscribed in ⨀A with a vertex at B, carry out the following step:
- Draw the segment between B and D.
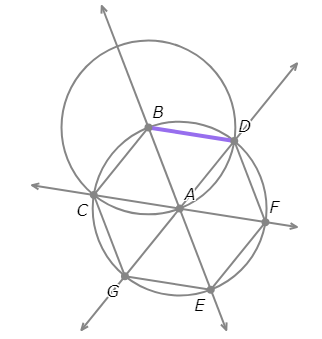

This means the six triangles formed by the segments between A and these six points are all isosceles.
Now, since △ABC and △ABD are equilateral triangles, m∠BAC and m∠BAD are both 60°. Find m∠CAG using the fact that these three angles form a straight angle.
m∠CAG = 180°–m∠BAC–m∠BAD
= 180°–60°–60°
= 60°
By the vertical angle theorem, it follows that m∠EAG, m∠EAF, and m∠DAF are all 60°. An isosceles triangle containing a 60° angle is equilateral, so △ABC, △ACG, △AEG, △AEF, △ADF and △ABD are all equilateral. Since each of these triangles has a side in common, they are all congruent equilateral triangles.
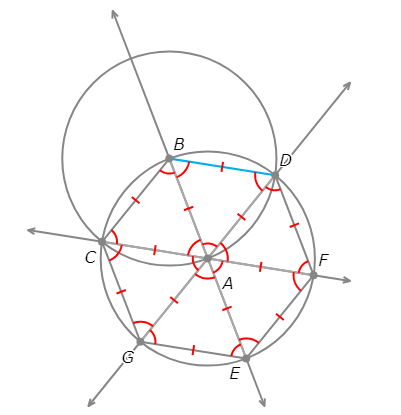
- So, all sides and interior angles of hexagon BCGEFD are congruent to each other. In other words, BCGEFD is a regular hexagon.
Let’s practice!🖊️

