The diagram below shows a nearly completed construction of a tangent to ⨀A (the smaller one) through B. Complete the construction.

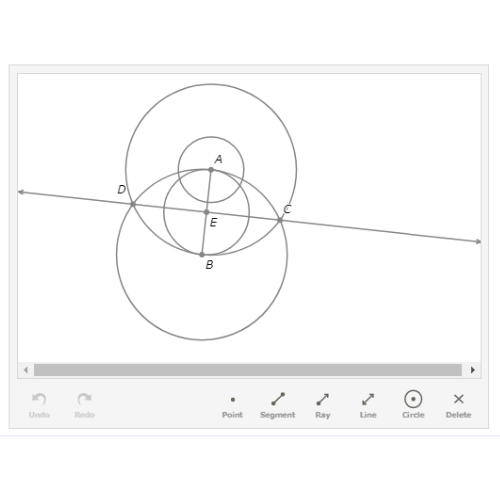
Part of the construction was done for you. Here are the steps to create this part of the construction.

Start with the objects in the diagram below.

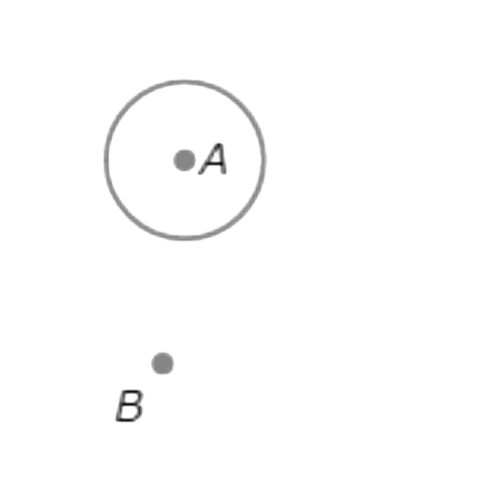
Find the midpoint of AB.

• Draw the segment between A and B.

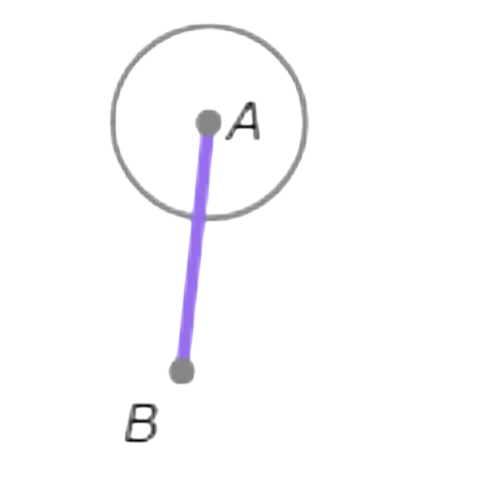
Draw a circle with radius AB centred at A.

Draw a circle with radius AB centred at B.

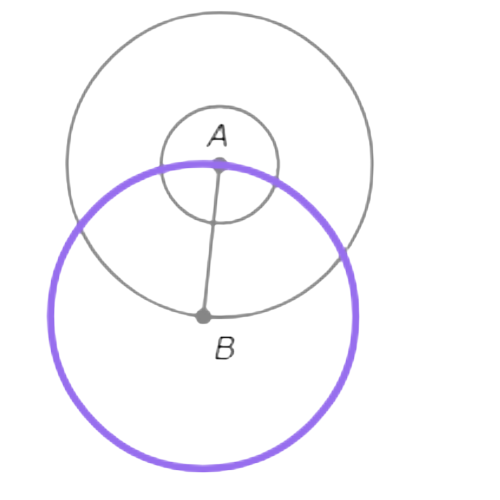
Mark the points where ⨀A (with radius AB) and ⨀B intersect. Call them C and D.

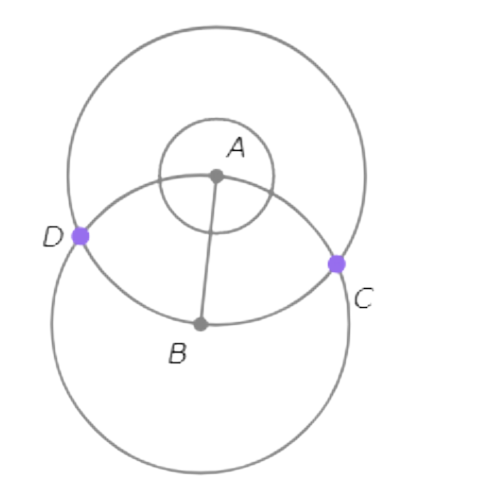
Since B and C are both on ⨀A,AB=AC. Since A and C are both on ⨀B,AB=BC. So, AB=AC=BC.

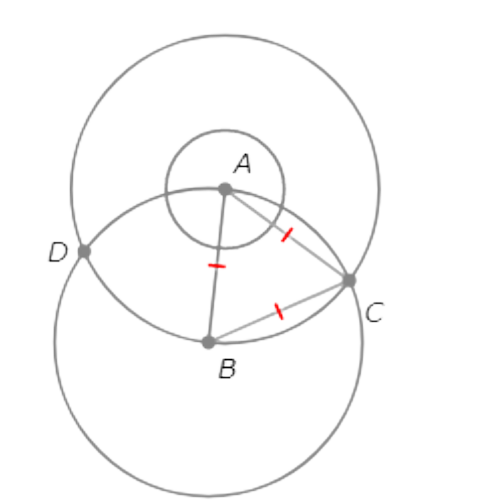
Similarly, AB=AD=BD.

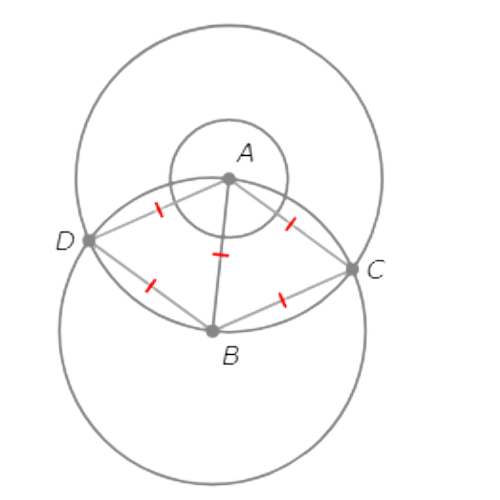
So, C and D are equidistant from A and B.

• Draw the line through C and D.

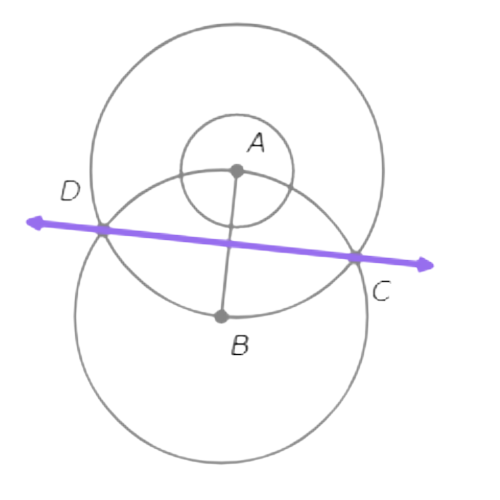
Recall that the set of points equidistant from 

A and B form the perpendicular bisector of AB. Since C and D are equidistant from A and B, they lie on the perpendicular bisector. So, CD is the perpendicular bisector of AB.